Question

【题目】抛物线y=x2+bx+c与x轴交于A（1，0），B（m，0），与y轴交于C．

（1）若m=﹣3，求抛物线的解析式，并写出抛物线的对称轴；

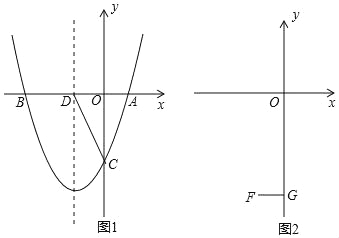
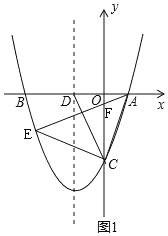
（2）如图1，在（1）的条件下，设抛物线的对称轴交x轴于D，在对称轴左侧的抛物线上有一点E，使S△ACE= S△ACD，求点E的坐标；

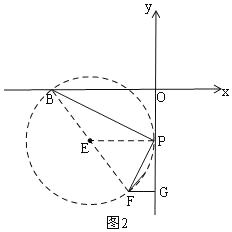
（3）如图2，设F（﹣1，﹣4），FG⊥y于G，在线段OG上是否存在点P，使∠OBP=∠FPG？若存在，求m的取值范围；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线的解析式为：y=x2+2x﹣3=（x+1）2﹣4；对称轴是：直线x=﹣1；（2）点E的坐标为E（﹣4，5）（3）当﹣4≤m＜0或m=3时，在线段OG上存在点P，使∠OBP=∠FPG.

【解析】

试题分析：（1）利用待定系数法求二次函数的解析式，并配方求对称轴；（2）如图1，设E（m，m2+2m﹣3），先根据已知条件求S△ACE=10，根据不规则三角形面积等于铅直高度与水平宽度的积列式可求得m的值，并根据在对称轴左侧的抛物线上有一点E，则点E的横坐标小于﹣1，对m的值进行取舍，得到E的坐标；

（3）分两种情况：①当B在原点的左侧时，构建辅助圆，根据直径所对的圆周角是直角，只要满足∠BPF=90°就可以构成∠OBP=∠FPG，如图2，求出圆E与y轴有一个交点时的m值，则可得取值范围；②当B在原点的右侧时，只有△OBP是等腰直角三角形，△FPG也是等腰直角三角形时满足条件，直接计算即可．

试题解析：（1）当m=﹣3时，B（﹣3，0），

把A（1，0），B（﹣3，0）代入到抛物线y=x2+bx+c中得：，解得，

∴抛物线的解析式为：y=x2+2x﹣3=（x+1）2﹣4；对称轴是：直线x=﹣1；

（2）如图1，设E（m，m2+2m﹣3），

由题意得：AD=1+1=2，OC=3，

S△ACE=S△ACD=×ADOC=×2×3=10，

设直线AE的解析式为：y=kx+b，

把A（1，0）和E（m，m2+2m﹣3）代入得，

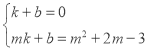，解得：，

∴直线AE的解析式为：y=（m+3）x﹣m﹣3，∴F（0，﹣m﹣3），

∵C（0，﹣3），∴FC=﹣m﹣3+3=﹣m，∴S△ACE=FC（1﹣m）=10，

﹣m（1﹣m）=20，m2﹣m﹣20=0，

（m+4）（m﹣5）=0，

m1=﹣4，m2=5（舍），

∴E（﹣4，5）；

（3）如图2，当B在原点的左侧时，连接BF，以BF为直径作圆E，当⊙E与y轴相切时，设切点为P，

∴∠BPF=90°，∴∠FPG+∠OPB=90°，∵∠OPB+∠OBP=90°，∴∠OBP=∠FPG，

连接EP，则EP⊥OG，

∵BE=EF，∴EP是梯形的中位线，∴OP=PG=2，

∵FG=1，tan∠FPG=tan∠OBP=，

∴，∴m=﹣4，

∴当﹣4≤m＜0时，在线段OG上存在点P，使∠OBP=∠FPG；

如图3，当B在原点的右侧时，要想满足∠OBP=∠FPG，

则∠OBP=∠OPB=∠FPG，∴OB=OP，

∴△OBP是等腰直角三角形，△FPG也是等腰直角三角形，

∴FG=PG=1，∴OB=OP=3，∴m=3，

综上所述，当﹣4≤m＜0或m=3时，在线段OG上存在点P，使∠OBP=∠FPG．