Question

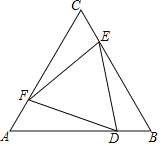
【题目】如图，一张正三角形的纸片的边长为2cm，D、E、F分别是边AB、BC、CA（含端点）上的点，设BD＝CE＝AF＝x（cm），△DEF的面积为y（cm2）．

（1）求y关于x的函数表达式和自变量的取值范围；

（2）求△DEF的面积y的最大值和最小值．

Answer 1

【答案】（1）y＝；（2）△DEF的面积的最大值为，最小值为

【解析】

（1）根据题意可知△AEG≌△BEF≌△CFG三个三角形全等，且在在△ADF中，AF＝x，AD＝2﹣x；可得△DEG的面积y与x的关系；

（2）利用二次函数的性质解决问题即可．

解：（1）∵AF＝BD＝CE＝x，且等边△ABC的边长为2，

∴BE＝CF＝AD＝2﹣x，

∵AB＝BC＝AC，

∴△ADF≌△BED≌△CFE（SAS）．

过点F做FM⊥AD

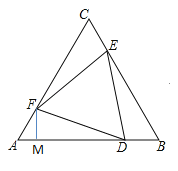
在△ADF中，AF＝x，AD＝2﹣x，

∵S△ADF＝ =AD×AF×sinA＝x（2﹣x）；

∴

∴y＝．

（2）∵y＝

∴其图象为二次函数，且开口向上，

∵0≤x≤2，

∴当x=1时，y有最小值为

当x=0或2时，y有最大值为

∴△DEF的面积的最大值为，最小值为．