题目内容

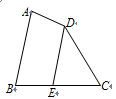
如图，矩形ABCD中，AB＝3，BC＝5，过对角线交点O作OE⊥AC交AD于E，则AE的长是（   ）．
A．1.6B．2.5C．3D．3.4
D
连接EC，由矩形的性质可得AO=CO，
又因EO⊥AC，则由线段的垂直平分线的性质可得EC=AE，
设AE=x，则ED=AD-AE=5-x，在Rt△EDC中，根据勾股定理可得EC2=DE2+DC2，
即x2=（5-x）2+32，解得x=3.4．故选D．
练习册系列答案
相关题目
如图，在四边形ABCD中，点E在BC上，AB∥DE，∠B＝78º，∠C＝60º，则∠EDC的度数为（ ▲ ）
A．78ºB．60ºC．42ºD．80º
菱形中，，，则对角线的长是（    ）
A．20B．15C．10D．5
如图，□ABCD中，∠C＝108°，BE平分∠ABC，则∠AEB=   （▲）
A．18°B．36°C．72°D．108°
（本题满分10分）如图1，在△ABC中，AB＝BC＝5，AC="6." △ECD是△ABC沿BC方向平移得到的，连接AE.AC和BE相交于点O.

（1）判断四边形ABCE是怎样的四边形，说明理由；
（2）如图2，P是线段BC上一动点（图2），（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化？
若变化，请说明理由；若不变，求出四边形PQED的面积；
②当线段BP的长为何值时，△PQR与△BOC相似？
如图，把边长为1的正方形ABCD绕顶点A逆时针旋转30o得到正方形AB′C′D′，则它们的公共部分的面积等于       ．
如图，正方形硬纸片ABCD的边长是4cm，点E、F分别是AB、BC的中点，若沿左图中的虚线剪开，拼成右图的一栋“小别墅”，则图中阴影部分的面积和是（    ）.
 
（A）2    （B）4    （C）8     （D）10
、如图，正方形ABCD边长为6， MN∥BC分别交AB、CD于点M、N，在MN上任取两点P、Q，那么图中阴影部分的面积是_______。
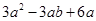长方形面积是，一边长为，则它的周长是（    ）.
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网