��Ŀ����
����Ŀ��һ�п쳵�ɼؿ����ҵأ�һ���������ҵؿ����أ�����ͬʱ�����������˶����쳵���ҵصľ���y1��km������ʻ��ʱ��x��h��֮��ĺ�����ϵ��ͼ1���߶�AB��ʾ���������ҵصľ���y2��km������ʻ��ʱ��x ��h��֮��ĺ�����ϵ��ͼ1���߶�OC��ʾ������ͼ����������о���
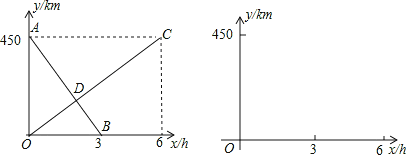
��1���ֱ����߶�AB��OC��Ӧ�ĺ�������ʽy1��y2��
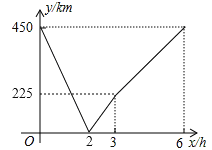
��2����졢����֮��ľ���ΪS����S��km����������ʻʱ��x��h���ĺ�����ϵʽ��������������ͼ��
��3����졢����֮��ľ��볬��135kmʱ��x��ȡֵ��Χ��
���𰸡���1��y1=-150x+450��y2=75x����2��S==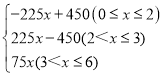 ��3��0��x��1.4��2.6��x��6��
��3��0��x��1.4��2.6��x��6��
��������
�����������1�����õ�A����Ϊ��0��450�������Եó��ף�������֮��ľ���Ϊ450�����õ�A����Ϊ��0��450������B����Ϊ��3��0��������y1=kx+b������ɣ������߶�OC����ʽΪy=ax������ɣ�
��2�����ã�1��������ó�S=|y1-y2|�����������������ʽ���ó�ͼ�ɣ�
��3��S=135ʱ�������������-225x+450=135��225x-450=135����ã�x=1.4��x=2.6��졢����֮��ľ��볬��135kmʱ��x��ȡֵ��Χ��0��x��1.4��2.6��x��6��
�����������1�����߶�AB�ĺ�������ʽΪy1=kx+b��
�ѵ�A����Ϊ��0��450������B����Ϊ��3��0��������y1=kx+b�ã� ![]()
��ã�![]()
��y1=-150x+450��
���߶�OC�ĺ�������ʽΪy=ax��
�ѣ�6��450������y=ax�ã�6a=450��
��ã�a=75��
��y2=75x��
��2�����ݣ�1���ó���
S=|y1-y2|=|450-150x--75x|=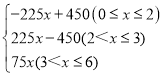
����ͼ����ͼ��ʾ��
��3��S=135ʱ�������������
-225x+450=135��225x-450=135��
��ã�x=1.4��x=2.6
��졢����֮��ľ��볬��135kmʱ��x��ȡֵ��Χ��0��x��1.4��2.6��x��6��

 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�