题目内容
如图,是一个上、下两部分均为圆柱体的容器,现向其中注水,直到注满为止,容器中水的体积v(cm3)随水面高度h(cm)变化的图象如下.
(1)求容器下部分圆柱体的高和底面圆的半径;
(2)求水的体积v(cm3)与水面高度h(cm)的函数关系式,并写出h的取值 范围.(圆柱体的体积v=πr2h,其中r是柱体底面圆的半径,h是圆柱的高)
范围.(圆柱体的体积v=πr2h,其中r是柱体底面圆的半径,h是圆柱的高)
解 (1)容器下部分圆柱体的高h=4 cm,由 36π=πr2•4 得底面圆的半径r=3.
(2)当0<h≤4时,v=9πh;
设 v=kh+b(k≠0).
当 h=4时,v=36π,∴4k+b=36π. ①
当h=6时,v=44π,∴6k+b=44π. ②
联立①、②,解得 k=4π,b=20π,∴v=4πh+20π.
故 ….
….
分析:(1)首先根据图象可以直接得到h的值;再根据圆柱体的体积公式:V=Sh=πr2h,把36π,h=4代入公式即可求出底面圆的半径;
(2)根据图象可以设出关系式 v=kh+b和v=kh,再把(4,36π)(6,44π)代入可以求出k,b的值,进而可得到关系式.
点评:此题主要考查函数图象,求一次函数关系式,关键是根据图象可以得到函数关系式设何种函数形式,然后利用待定系数法求值即可.
(2)当0<h≤4时,v=9πh;
设 v=kh+b(k≠0).
当 h=4时,v=36π,∴4k+b=36π. ①
当h=6时,v=44π,∴6k+b=44π. ②
联立①、②,解得 k=4π,b=20π,∴v=4πh+20π.
故
 ….
….分析:(1)首先根据图象可以直接得到h的值;再根据圆柱体的体积公式:V=Sh=πr2h,把36π,h=4代入公式即可求出底面圆的半径;
(2)根据图象可以设出关系式 v=kh+b和v=kh,再把(4,36π)(6,44π)代入可以求出k,b的值,进而可得到关系式.
点评:此题主要考查函数图象,求一次函数关系式,关键是根据图象可以得到函数关系式设何种函数形式,然后利用待定系数法求值即可.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目

 范围.(圆柱体的体积v=πr2h,其中r是柱体底面圆的半径,h是圆柱的高)
范围.(圆柱体的体积v=πr2h,其中r是柱体底面圆的半径,h是圆柱的高)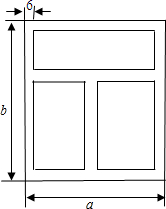 如图,一个用铝合金材料加工的长方形窗框,它的宽和高分别为a厘米,b厘米,解答下列问题(结果可用含a,b的代数式表示).
如图,一个用铝合金材料加工的长方形窗框,它的宽和高分别为a厘米,b厘米,解答下列问题(结果可用含a,b的代数式表示).