Question

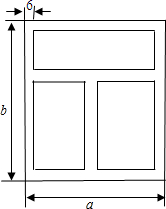如图，一个用铝合金材料加工的长方形窗框，它的宽和高分别为a厘米，b厘米，解答下列问题（结果可用含a，b的代数式表示）．
（1）长方形窗框的面积是

ab

厘米²；
（2）铝合金窗分为上、下两栏，四周框架和中间隔栏的材料均为宽度6厘米的铝合金材料，上栏和下栏的框内高度（不含铝合金部分）的比为1：2（接口用料忽略不计）．
①求制作一个该种窗框所需铝合金材料的总长度；
②求该种窗框的透光部分的面积．

Answer 1

分析：（1）先根据题意宽和高分别为a厘米，b厘米，即可求出长方形窗框的面积；
（2）①根据题意先求出上栏框内高度和下栏框内高度，即可求出该种窗框所需铝合金材料的总长度； ②先根据题意和（1）即可求出透光部分的面积；

解答：解：（1）根据题意可得：
a•b=ab
（2）①∵上栏和下栏的框内高度（不含铝合金部分）的比为1：2，
上栏和下栏的框内高度（不含铝合金部分）的和是b-6×3=b-18，
∴上栏框内高度是

b-18

3

厘米，
 下栏框内高度

2(b-18)

3

厘米，
长方形窗框竖直部分所需铝合金材料长度是3（a-12）厘米，
∴总长度2b+3（a-12）+

2(b-18)

3

，
=（3a+

8

3

b-48）厘米，
②根据题意得：
透光部分的面积=ab-6（3a+

8

3

b-48），
=（ab-18a-16b+288）厘米²；
故答案为：ab．

点评：本题考查了列代数式；此题实际问题转化为数学问题的能力，同时考查利用基本不等式求函数的最值注意满足的条件：一正、二定、三相等，属于中档题．