题目内容
如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于A、B两点,
的图像相交于A、B两点,
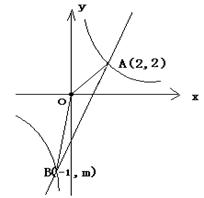
(1)利用图中条件,求反比例函数和一次函数的解析式。
(2)根据图像写出使一次函数的值小于反比例函数的值的![]() 的取值范围。
的取值范围。
(3)求△AOB的面积。
(1)y=![]() ,y=2x—2(2)x< —1或0<x<2(3)3
,y=2x—2(2)x< —1或0<x<2(3)3
解析:(1)因为A,B两点都在两图像上,代入两函数,可求得两函数的关系式。
解:由图可知y=![]() 过点A(2.2),B(—1,m).把A(2.2)代入y=
过点A(2.2),B(—1,m).把A(2.2)代入y=![]() 得:
得:
2=![]() ,n=4 , 所以反比例函数的关系式为:y=
,n=4 , 所以反比例函数的关系式为:y=![]()
把B(—1,m)代入y=![]() 得:m=
得:m=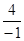 = —4
= —4
所以点B的坐标为(—1,—4)
把点A(2.2)和点B(—1,—4)代入y=kx+b得:
![]() 解得:
解得:![]()
因此一次函数的关系式为:y=2x—2
(2)由图象可知:当x< —1或0<x<2时,一次函数的的值小于反比例函数的值。
(3)△AOB的面积可看成两三角形的和求解。
设一次函数y=2x—2与y轴的交点为点G,则点G的坐标为(0,—2)
则线段OG=|—2|=2
S△BOG=|—2|×|—1|×![]() =1
=1
S△AOG=|—2|×|2|×![]() =2
=2
所以:S△AOB= S△BOG + S△AOG=1+2=3

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
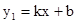 的图像与反比例函数
的图像与反比例函数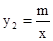 的图像相交于A、B两点,
的图像相交于A、B两点,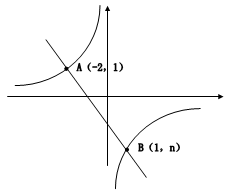
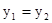
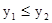
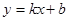 的图像与反比例函数
的图像与反比例函数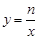 的图像相交于A、B两点,
的图像相交于A、B两点,
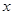 的取值范围。
的取值范围。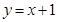 的图像与
的图像与 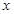 轴、
轴、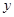 轴分别相交于点
轴分别相交于点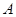 、
、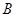 .二次函数的图像与
.二次函数的图像与 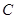 ,与这个一次函数的图像相交于点
,与这个一次函数的图像相交于点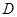 ,
,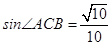 .
.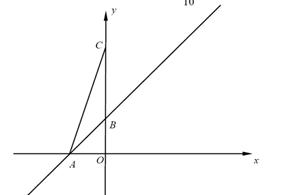
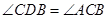 ,求这个二次函数的解析式.
,求这个二次函数的解析式.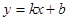 的图像与反比例函数
的图像与反比例函数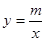 的图像交于
的图像交于 两点。
两点。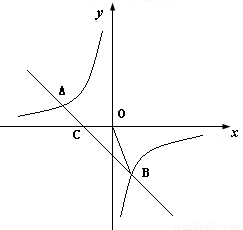
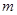 的值;
的值;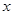 轴于点C,求△OBC的面积.
轴于点C,求△OBC的面积.