Question

【题目】如图，已知为的直径，线段是的弦且，与相切于点，为直径，连接，．

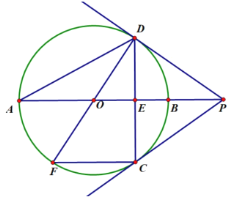
（1）求证：与相切；

（2）求证：；

（3）若，，求的值和线段的长．

Answer 1

【答案】（1）见解析；（2）见解析；（2），

【解析】

（1）连接OC．欲证PC是⊙O的切线，只需证明OC⊥PC即可；通过全等三角形△COP≌△DOP（SAS）的对应角∠OCP=∠ODP=90°来证明该结论；

（2）先证得△ODE△OPD，得到，根据OD是半径，AB是直径，即可证明结论；

（3）利用三角形中位线定理求得OE=3，设⊙O为R，利用勾股定理得到，再在Rt中利用构建方程即可求得R的值，在Rt中可求得的值，利用（2）的结论可求得PO的长，从而求得线段的长．

（1）连接OC，

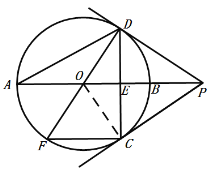
∵在⊙O中，OD=OC，AB⊥CD于点E，
∴∠COP=∠DOP．
在△OCP和△ODP中，

，

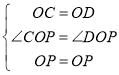∴△OCP≌△ODP（SAS）．
∴∠OCP=∠ODP，
又∵PD切⊙O于点D，OD为⊙O半径，
∴OD⊥PD，
∴∠ODP=90°，
∴∠OCP=90°，
∴OC⊥PC于点C，
∴PC是⊙O的切线；

（2）∵PD切⊙O于点D，

∴∠ODP=90°，
∵AB⊥CD于点E，
∴∠OED=90°，

∴Rt△ODERt△OPD，

∴，

∴，

∵OD是⊙O的半径，AB是⊙O的直径，

∴OD=AB，

∴，

即：；

（3）∵DF是⊙O的直径，

∴∠FCD=90°，

∵∠OED=90°，

∴OE∥FC，

又∵DO=OF，

∴OE=FC=3，

设⊙O为R，

在Rt中：，则，

在Rt中，AE=R+3，

∵，

∴，

∴R+3=2，

解得：R=5(负值已舍)，

在Rt中，FD=2R=10，FC=6，

∴，

由（2）得：，

即，

∴，

∴．