Question

如图，AB为半圆的直径，点P为AB上一动点，动点P从点A出发，沿AB匀速运动到点B，运动时间为t，分别以AP与PB为直径做半圆，则图中阴影部分的面积S与时间t之间的函数图象大致为（　　）

• A、
• B、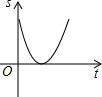
• C、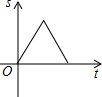
• D、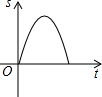

Answer 1

分析：按等量关系“阴影面积=以AB为直径的半圆面积-以AP为直径的半圆面积-以PB为直径的半圆面积”列出函数关系式，然后再判断函数图象．

解答：解：设P点运动速度为v（常量），AB=a（常量），则AP=vt，PB=a-vt；
则阴影面积S=

1

2

π(

a

2

)2-

1

2

π(

vt

2

)2-

1

2

π(

a-vt

2

)2=

π(-v2t2+avt)

4

=-

πv2

4

t2+

πav

4

t
由函数关系式可以看出，D的函数图象符合题意．
故选D．

点评：本题考查的是面积随动点匀速运动时变化的关系，关键是列出函数关系式，再与函数图象对照．