题目内容
(12分)如图所示,一内壁光滑的细管弯成半径为R=0.4 m的半圆形轨道CD,竖直放置,其内径略大于小球的直径,水平轨道与竖直半圆轨道在C点连接完好.置于水平轨道上的弹簧左端与竖直墙壁相连,B处为弹簧的自然状态.将一个质量为m=0.8 kg的小球放在弹簧的右侧后,用力向左侧推小球而压缩弹簧至A处,然后将小球由静止释放,小球运动到C处后对轨道的压力为F1=58 N.水平轨道以B处为界,左侧AB段长为x=0.3 m,与小球的动摩擦因数为μ=0.5,右侧BC段光滑.g=10 m/s2,求:
(1)弹簧在压缩时所储存的弹性势能.
(2)小球运动到轨道最高处D点时对轨道的压力.
(1)11.2 J (2)10 N,方向向上解析:
(1)对小球在C处,由牛顿第二定律及向心力公式得
F1-mg=m
v1==m/s=5 m/s
从A到B由动能定理得Ep-μmgx=mv12
Ep=mv12+μmgx=×0.8×52 J+0.5×0.8×10×0.3 J=11.2 J.
(2)从C到D由机械能守恒定律得
mv12=2mgR+mv22
v2== m/s=3 m/s
由于v2>=2 m/s,所以小球在D处对轨道外壁有压力.
小球在D处,由牛顿第二定律及向心力公式得
F2+mg=m
F2=m(-g)=0.8×(-10) N=10 N.
由牛顿第三定律得小球对轨道压力为10 N.
(1)对小球在C处,由牛顿第二定律及向心力公式得
F1-mg=m
v1==m/s=5 m/s
从A到B由动能定理得Ep-μmgx=mv12
Ep=mv12+μmgx=×0.8×52 J+0.5×0.8×10×0.3 J=11.2 J.
(2)从C到D由机械能守恒定律得
mv12=2mgR+mv22
v2== m/s=3 m/s
由于v2>=2 m/s,所以小球在D处对轨道外壁有压力.
小球在D处,由牛顿第二定律及向心力公式得
F2+mg=m
F2=m(-g)=0.8×(-10) N=10 N.
由牛顿第三定律得小球对轨道压力为10 N.

练习册系列答案
相关题目

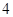 ,
,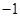 )的抛物线交
)的抛物线交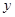 轴于
轴于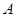 点,交
点,交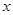 轴于
轴于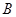 ,
,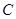 两点(点
两点(点 ,
,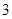 ).
).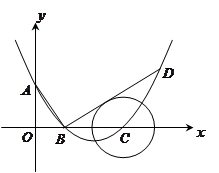
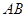 的垂线交抛物线于点
的垂线交抛物线于点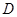 ,
,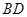 相切,请判断抛物
相切,请判断抛物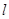 与⊙
与⊙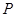 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于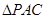 的
的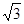 ,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线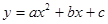 过点A、E、D.
过点A、E、D.
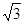 ,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线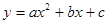 过点A、E、D.
过点A、E、D.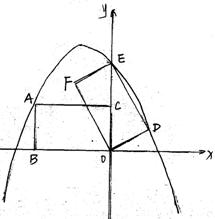
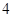 ,
,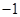 )的抛物线交
)的抛物线交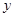 轴于
轴于 点,交
点,交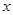 轴于
轴于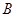 ,
,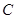 两点(点
两点(点 ,
,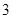 ).
).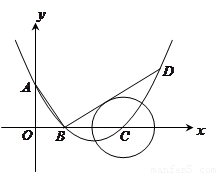
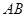 的垂线交抛物线于点
的垂线交抛物线于点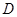 ,
,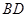 相切,请判断抛物
相切,请判断抛物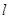 与⊙
与⊙ 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 的
的