题目内容
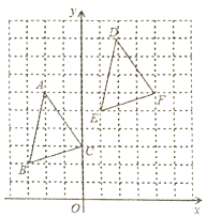
【题目】已知:如图,点![]() 在
在![]() 的一边
的一边![]() 上,过点
上,过点![]() 的直线
的直线![]() ,
,![]() 平分
平分![]() ,
,![]() 于
于![]() .
.

![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 求证:
求证:![]() 平分
平分![]() ;
;
【答案】(1)110°;(2)证明见详解
【解析】
(1)根据平行线的性质,得到∠ACE=40°,根据平角的定义以及角平分线的定义,即可得到∠ACF=70°,进而得出∠ECF的度数;
(2)根据∠DCG+∠DCF=90°,∠GCO+∠FCA=90°,以及∠ACF=∠DCF,运用等角的余角相等,即可得到∠GCO=∠GCD,即CG平分∠OCD
解:(1)∵DE∥OB,
∴∠O=∠ACE,(两直线平行,同位角相等)
∵∠O=40°,
∴∠ACE=40°,
∵∠ACD+∠ACE=180°,(平角定义)
∴∠ACD=140°,
又∵CF平分∠ACD,
∴∠ACF=70°,(角平分线定义)
∴∠ECF=70°+40°=110°;
(2)证明:∵CG⊥CF,
∴∠FCG=90°,
∴∠DCG+∠DCF=90°,
又∵∠AOC=180°,(平角定义)
∴∠GCO+∠FCA=90°,
∵∠ACF=∠DCF,
∴∠GCO=∠GCD,(等角的余角相等)
即CG平分∠OCD.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案【题目】小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)在这三次购物中,第 次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
【题目】某校举行“汉字听写”比赛,全体学生都参与,每名学生听写39个汉字,比赛结束后,学校随机抽查了部分学生的听写结果,绘制成如下所示的统计表(不完整)和如图所示的统计图(不完整) .请根据题意解答下列问题.
组别 | 正确的个数x | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
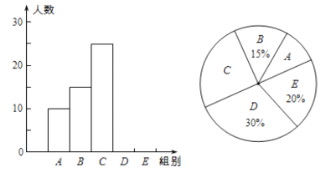
(1)统计表中的m=__,n=___;
(2)请补全频数分布直方图:
(3)在扇形统计图中,C组所对应扇形的圆心角的度数是______ ;
(4)已知该校共有1260名学生,如果听写汉字正确的个数少于24定为不合格,那么该校本次比赛不合格的学生人数大约是多少?