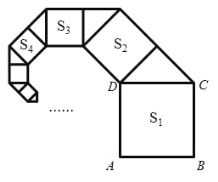
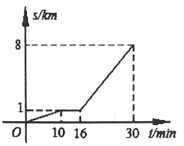
题目内容
【题目】如图,直线ll,l2交于点O,点P关于ll,l2的对称点分别为P1、P2.
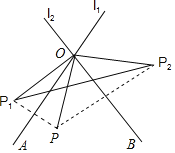
(1)若ll,l2相交所成的锐角∠AOB=60°,则∠P1OP2=______;
(2)若OP=3,P1P2=5,求△P1OP2的周长.
【答案】(1)120°;(2)△P1OP2的周长=11.
【解析】
(1)由于P关于l1、l2的对称点分别为P1、P2,可得出∠P1AO=∠AOP,∠P2OB=∠POB,再根据∠AOB=60°即可求解;
(2)根据对称的性质可知,OP1=OP=OP2=3,再根据P1P2=5即可求出△P1OP2的周长.
解:(1)∵P关于l1、l2的对称点分别为P1、P2,
∴∠P1OA=∠AOP,∠P2OB=∠POB,
∴∠P1OP2=2(∠AOP+∠POB)=2∠AOB=2×60°=120°;
故答案为:120°;
(2)∵P关于l1、l2的对称点分别为P1、P2,
∴OP1=OP=OP2=3,
∵P1P2=5,
∴△P1OP2的周长=OP1+OP2+P1P2=3+3+5=11.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目