题目内容
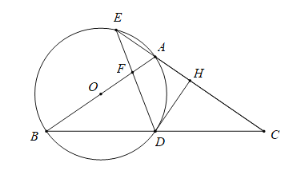
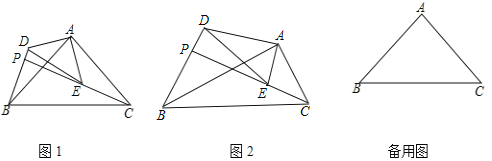
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,过
上一点,过![]() 、
、![]() 分别作
分别作![]() 、
、![]() 的平行线交于点
的平行线交于点![]() ,联结
,联结![]() 并延长,与射线
并延长,与射线![]() 交于点
交于点![]() .
.
(1)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)当点![]() 在边
在边![]() .上时,设
.上时,设![]() ,求
,求![]() 的面积;(用含
的面积;(用含![]() 的代数式表示)
的代数式表示)
(3)当![]() 时,求
时,求![]() 的余弦值.
的余弦值.
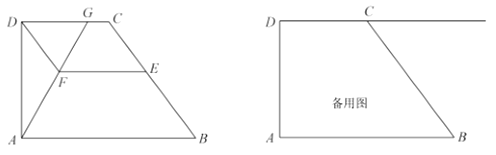
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意可得四边形DCEF是平行四边形,可得CD=EF,通过证明△CFE∽△CAB进行分析求值即可;
(2)根据题意延长AG,BC交为于点M,过点C作CN⊥AB于点N,交EF于点H,由题意可得四边形ADCN是矩形,可得AD=CN=4,CD=AN=3,BN=3,由平行线分线段成比例可求BE,ME,MC,CH,GC的长,即可求GD的长,由三角求形面积公式可△DFG的面积;
(3)根据题意由△AFD∽△ADG,可得∠AFD=∠ADG=90°,由余角的性质可得∠DAG=∠B,即可求∠DAG的余弦值.
解:(1)如图,
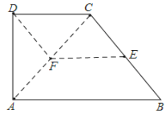
∵DC∥EF,DF∥CE,
∴四边形DCEF是平行四边形,
∴CD=EF,
∵AB=2CD=6,
∴AB=2EF,
∵EF∥CD,AB∥CD,
∴EF∥AB,
∴△CFE∽△CAB,
∴![]() ,
,
∴BC=2CE,
∴BE=CE,
∴EC:BE=1:1=1.
(2)如图,延长AG,BC交为于点M,过点C作CN⊥AB于点N,交EF于点H,
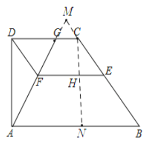
∵AD⊥CD,CN⊥CD,
∴AD∥CN,且CD∥AB,
∴四边形ADCN是平行四边形,
又∵∠DAB=90°,
∴四边形ADCN是矩形,
∴AD=CN=4,CD=AN=3,
∴BN=AB-AN=3,
在Rt△BCN中,BC=![]() ,
,
∴BE=BC-CE=5-m,
∵EF∥AB,
∴![]() 即
即![]() ,
,
∴ME=BE=5-m,
∴MC=ME-CE=5-2m,
∵EF∥AB,
∴![]() ,
,
∴HC=![]() ,
,
∵CG∥EF,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)过点C作CN⊥AB于点N,
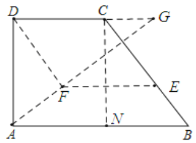
∵AB∥CD,∠DAB=90°,
∴∠DAB=∠ADG=90°,
若△AFD∽△ADG,
∴∠AFD=∠ADG=90°,
∴DF⊥AG,
又∵DF∥BC,
∴AG⊥BC,
∴∠B+∠GAB=90°,且∠DAG+∠GAB=90°,
∴∠B=∠DAG,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案