Question

①计算：

4

-2×(-

1

2

)-1+|tan45°-2|-(

2

-1)°
②先化简，再求值．

x2-2x

x2-1

÷(x-1-

2x-1

x+1

)，其中x=

1

2

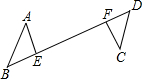
③如图，AB∥CD，AB=CD，点B、E、F、D在一条直线上，∠A=∠C．求证：AE=CF．

Answer 1

分析：（1）首先计算开方以及乘方运算，最后进行加减运算即可；
（2）化简时首先运算括号内的式子，把除法转化成乘法，即可化简，然后代入数据计算即可；
（3）首先根据平行线的性质证得：∠B=∠D，然后根据ASA即可证得两个三角形全等．

解答：解：（1）原式=2-2×（-2）+|1-2|-1 
=2+4+1-1　　　　　　　
=6，
（2）原式=

x2-2x

x2-1

÷(

x2 -1

x+1

-

2x-1

x+1

)
=

x(x-2)

(x-1)(x+1)

×(

x+1

x(x-2)

)
=

1

x-1

当x=

1

2

时，原式=

1

1 2 -1

=

1

- 1 2

=-2，
（3）证明：∵AB∥CD
∴∠B=∠D
在△ABE和△CDF中．
∵

∠A=∠C AB=CD ∠B=∠D

∴△ABE≌△CDF．
∴AE=CF．

点评：本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算．