题目内容
 (2013•咸宁模拟)操作探究题:
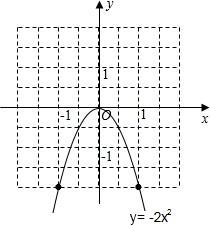
(2013•咸宁模拟)操作探究题:(1)在平面直角坐标系x0y中,画出函数y=-2x2的图象;
(2)将抛物线y=-2x2怎样平移,使得平移后的抛物线满足:①过原点,②抛物线与x正半轴的另一个交点为Q,其顶点为P,且∠OPQ=90°;并写出抛物线的函数表达式;
(3)在上述直角坐标系中,以O为圆心,OP为半径画圆,交x轴于A、B(A点在左边)两点,在抛物线(2)上是否存在一点M,使S△MOA:S△POB=2:1?若存在,求出M点的坐标;若不存在,说明理由.
(4)在(3)的条件下,是否存这样的直线过A点且与抛物线只有一个交点?若存在,直接写出其解析式.若不存在,说明理由.
分析:(1)取函数图象上的三个不同点,通过描点、连线进行作图即可.
(2)由于Q、O关于新抛物线的对称轴对称,即点P在线段OQ的垂直平分线上,首先能判断出的是△OPQ一定是等腰三角形,若∠OPQ=90°,那么该三角形一定是等腰直角三角形,若设P(a、a),那么Q(2a,0),利用待定系数法可确定该函数的解析式,进一步可判断出平移方案.
(3)首先求出P、A、B的坐标,则△MOA、△POB的面积可知,根据三角形的面积公式即可得到M点的纵坐标,代入(2)的抛物线解析式中,可得到M点的完整坐标(注意M可能在x轴的上方和下方).
(4)分两种情况:①过点A且平行于y轴;②设出该直线的解析式,然后联立直线、抛物线的解析式组成方程,若两函数只有一个交点,那么方程的根的判别式为0,按此思路解答即可.
(2)由于Q、O关于新抛物线的对称轴对称,即点P在线段OQ的垂直平分线上,首先能判断出的是△OPQ一定是等腰三角形,若∠OPQ=90°,那么该三角形一定是等腰直角三角形,若设P(a、a),那么Q(2a,0),利用待定系数法可确定该函数的解析式,进一步可判断出平移方案.
(3)首先求出P、A、B的坐标,则△MOA、△POB的面积可知,根据三角形的面积公式即可得到M点的纵坐标,代入(2)的抛物线解析式中,可得到M点的完整坐标(注意M可能在x轴的上方和下方).
(4)分两种情况:①过点A且平行于y轴;②设出该直线的解析式,然后联立直线、抛物线的解析式组成方程,若两函数只有一个交点,那么方程的根的判别式为0,按此思路解答即可.
解答:解:(1)取(0,0)、(1,-2)、(-1,-2)三点,作图如下:
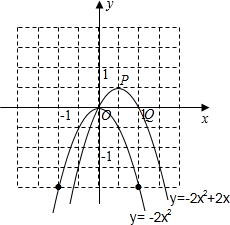 (2)由题意知:O、Q关于平移后的抛物线的对称轴对称,所以顶点P在OQ的垂直平分线上,即△OPQ是等腰三角形;
(2)由题意知:O、Q关于平移后的抛物线的对称轴对称,所以顶点P在OQ的垂直平分线上,即△OPQ是等腰三角形;
若∠OPQ=90°,那么△OPQ是等腰三角形,若设P(a,a),则Q(2a,0);
设抛物线的解析式为:y=-2(x-a)2+a,由于抛物线经过Q(2a,0),则:
-2a2+a=0,得:a=
或a=0;
∴抛物线的解析式为:y=-2(x-
)2+
;
平移方案:先将抛物线y=-2x2向右平移
个单位,再向上平移
个单位.
(3)由题意知:S△MOA=2S△POB,且OP=OA=OB;
S△OPB=
OB•|yP|=
×OB×
;
S△MOA=
OA•|yM|=
×OA×|yM|;
∴|yM|=2|yP|=1,即M点纵坐标为:-1(1舍去).
由(2)得抛物线的解析式为:y=-2x2+2x,当y=-1时:
-2x2+2x=-1,x1=
、x2=
;
∴存在符合条件的M点,且坐标为(
,-1)(
,-1).
(4)由(2)知:P(
,
),则OP=OA=
,A(-
,0);
①过点A且与y轴平行的直线:x=-
;
交(2)的抛物线于点(-
,-
-1);
②当该直线与y轴不平行时,设直线的解析式为:y=kx+b,由于过点A(-
,0),则有:
-
k+b=0,b=
k;
即:该直线的解析式:y=kx+
k,联立抛物线的解析式,得:
kx+
k=-2x2+2x,化简得:2x2+(k-2)x+
k=0
由于两函数只有一个交点,则:
△=(k-2)2-4×2×
k=k2-(4+4
)k+4=0,
解得:k=2+2
±2
∴y=(2+2
+2
)x+2+
+
或y=(2+2
-2
)x+2+
-
;
综上,符合条件的直线有三条:x=-
、y=(2+2
+2
)x+2+
+
或y=(2+2
-2
)x+2+
-
.

 (2)由题意知:O、Q关于平移后的抛物线的对称轴对称,所以顶点P在OQ的垂直平分线上,即△OPQ是等腰三角形;
(2)由题意知:O、Q关于平移后的抛物线的对称轴对称,所以顶点P在OQ的垂直平分线上,即△OPQ是等腰三角形;若∠OPQ=90°,那么△OPQ是等腰三角形,若设P(a,a),则Q(2a,0);
设抛物线的解析式为:y=-2(x-a)2+a,由于抛物线经过Q(2a,0),则:
-2a2+a=0,得:a=
| 1 |
| 2 |
∴抛物线的解析式为:y=-2(x-
| 1 |
| 2 |
| 1 |
| 2 |
平移方案:先将抛物线y=-2x2向右平移
| 1 |
| 2 |
| 1 |
| 2 |
(3)由题意知:S△MOA=2S△POB,且OP=OA=OB;
S△OPB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S△MOA=
| 1 |
| 2 |
| 1 |
| 2 |
∴|yM|=2|yP|=1,即M点纵坐标为:-1(1舍去).
由(2)得抛物线的解析式为:y=-2x2+2x,当y=-1时:
-2x2+2x=-1,x1=
1+
| ||
| 2 |
1-
| ||
| 2 |
∴存在符合条件的M点,且坐标为(
1+
| ||
| 2 |
1-
| ||
| 2 |
(4)由(2)知:P(
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
①过点A且与y轴平行的直线:x=-
| ||
| 2 |
交(2)的抛物线于点(-
| ||
| 2 |
| 2 |
②当该直线与y轴不平行时,设直线的解析式为:y=kx+b,由于过点A(-
| ||
| 2 |
-
| ||
| 2 |
| ||
| 2 |
即:该直线的解析式:y=kx+
| ||
| 2 |
kx+
| ||
| 2 |
| ||
| 2 |
由于两函数只有一个交点,则:
△=(k-2)2-4×2×
| ||
| 2 |
| 2 |
解得:k=2+2
| 2 |
2+2
|
∴y=(2+2
| 2 |
2+2
|
| 2 |
2
|
| 2 |
2+2
|
| 2 |
2
|
综上,符合条件的直线有三条:x=-
| ||
| 2 |
| 2 |
2+2
|
| 2 |
2
|
| 2 |
2+2
|
| 2 |
2
|
点评:该题的难度不大,主要考查的函数解析式的确定及图象的画法、函数图象的平移、图形面积的解法、函数图象交点坐标的求法等基础知识,(4)题中,与y轴平行的直线容易漏掉,这是该题的一个易错点.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 ,ab+a-b,ab+a+b可能成为有理数的个数有 个.
,ab+a-b,ab+a+b可能成为有理数的个数有 个.