题目内容
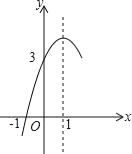
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
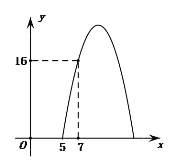
⑴a= ;b= ;
⑵销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
⑶由图象可知,销售单价x在 时,该种商品每天的销售利润不低于16元?
【答案】(1)-1,20;(2)当x=10时,该商品的销售利润最大,最大利润是25元;(3)7≤x≤13
【解析】
(1)利用待定系数法求二次函数解析式得出即可;
(2)利用配方法求出二次函数最值即可;
(3)根据题意令y=16,解方程可得x的值,结合图象可知x的范围.
解:(1)y=ax2+bx-75图象过点(5,0)、(7,16),
∴![]()
解得:![]()
故答案为-1,20
⑵∵![]()
∴当x=10时,该商品的销售利润最大,最大利润是25元.
⑶根据题意,当y=16时,得:-x2+20x-75=16,
解得:x1=7,x2=13,
即销售单价7≤x≤13时,该种商品每天的销售利润不低于16元.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
【题目】下表中给出![]() ,
,![]() ,
,![]() 三种手机通话的收费方式.
三种手机通话的收费方式.
收费方式 | 月通话费/元 | 包时通话时间/ | 超时费/(元/ |
|
|
|
|
|
|
|
|
|
| 不限时 |
(1)设月通话时间为![]() 小时,则方案
小时,则方案![]() ,
,![]() ,
,![]() 的收费金额
的收费金额![]() ,
,![]() ,
,![]() 都是
都是![]() 的函数,请分别求出这三个函数解析式.
的函数,请分别求出这三个函数解析式.
(2)填空:
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
(3)小王、小张今年![]() 月份通话费均为
月份通话费均为![]() 元,但小王比小张通话时间长,求小王该月的通话时间.
元,但小王比小张通话时间长,求小王该月的通话时间.