题目内容
在平面直角坐标系中,已知点A(3,2),B(-2,-3),则经过A,B两点函数图象的解析式可以为 (写出一个即可)
考点:反比例函数图象上点的坐标特征
专题:开放型
分析:可以设反比例函数解析式为y=
(k≠0),然后再把点A(3,2)代入函数解析式可得k的值,进而得到函数解析式.
| k |
| x |
解答:解:设反比例函数解析式为y=
(k≠0),
∵图象经过点A(3,2),
∴3×2=k,
k=6,
∴反比例函数解析式为y=
,
故答案为:y=
.
| k |
| x |
∵图象经过点A(3,2),
∴3×2=k,
k=6,
∴反比例函数解析式为y=
| 6 |
| x |
故答案为:y=
| 6 |
| x |
点评:本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
已知抛物线y=x2-x-1与x轴的一个交点为(-a,0),则代数式a2+a-12值为( )
| A、12 | B、11 |
| C、-11 | D、-12 |
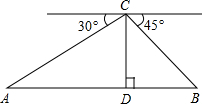 如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为50m,点A、D、B在同一条直线上,则A、B两点的距离是
如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为50m,点A、D、B在同一条直线上,则A、B两点的距离是 如图,已知∠1=∠2,要说明△ABC≌△BAD,可添加的条件是
如图,已知∠1=∠2,要说明△ABC≌△BAD,可添加的条件是