题目内容
【题目】如图，AB∥CD,AD∥BC,∠A﹦3∠B.求∠A、∠B、∠C、∠D的度数.
【答案】1350,450,1350,450
【解析】
根据AD∥BC,∠A=3∠B,
可得:∠A+∠B=180°,即4∠B=180°,解得∠B=45°,进而可得:∠A=3∠B=3×45°=135°,
再根据AB∥CD,可得:∠A+∠D=180°,∠B+∠C=180°,进而可得:∠D=180°-∠A=180°-135°=45°,∠C=180°-∠B=180°-45°=135°.
∵AD∥BC,∠A=3∠B,
∴∠A+∠B=180°,即4∠B=180°,解得∠B=45°,
∴∠A=3∠B=3×45°=135°,
∵AB∥CD,
∴∠A+∠D=180°,∠B+∠C=180°,
∴∠D=180°-∠A=180°-135°=45°,∠C=180°-∠B=180°-45°=135°,
答:∠A、∠B、∠C、∠D的度数分别为:135°,45°,135°,45°.
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
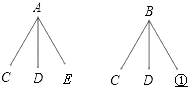
【题目】某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售．每种型号的打印机均需要一种芯片配套才能打印．
（1）下列是该店用树形图或列表设计的配套方案，①的位置应填写 ， ②的位置应 填写
（2）若仅有B型打印机与E种芯片不配套，则上面（1）中的方案配套成功率是
芯片 | C | D | E |
A | （A，C） | （A，D） | ② |
B | （B，C） | （B，D） | （B，E） |
