Question

（2012•永春县模拟）如图，要在一面靠墙（墙长11米）的空地上，用长为16米的篱笆围成一个矩形花圃（不靠墙一边不超过墙长），设与墙平行的一边BC的长为x米，面积为y平方米．
（1）直接写出：与墙垂直的一边AB的长；（用含x的代数式表示）
（2）若与墙平行的一边BC的长度不小于与墙垂直的一边AB的长度，问BC边应为多少米时，才能使矩形花圃ABCD所占地面面积最小，并求出此时最小的面积．

Answer 1

分析：（1）AB=（16-BC）÷2；
（2）表示出矩形的面积，求得自变量的取值范围，进而根据抛物线增减性得到所对应的最小的函数值即可．

解答：解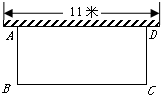：（1）AB=（16-x）÷2=8-

x

2

；
（2）设矩形ABCD的面积是y平方米，
y=x（8-

x

2

）=-

1

2

x²+8x=-

1

2

（x-8）²+32
依题意得：

x≥- 1 2 x+8 x≤11

，
解得：

16

3

≤x≤11
当

16

3

≤x＜8时，y随x的增大而增大
∴当x=

16

3

时，y有最小值为

256

9

当8＜x≤11时，y随x的增大而减少
∴当x=11时，y有最小值为

55

2

∵

256

9

＞

55

2

∴当x=11时y有最小值为

55

2

．

点评：考查二次函数的应用；注意根据自变量的取值及二次函数的增减性得到最小面积．