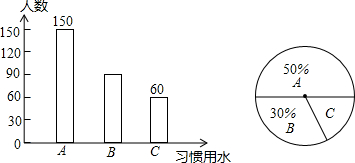
题目内容
 在数学课外活动中,某学习小组在讨论“导学案”上的一个作业题:
在数学课外活动中,某学习小组在讨论“导学案”上的一个作业题:
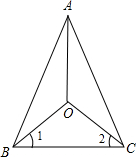
已知:如图,OA平分∠BAC,∠1=∠2.
求证:AO⊥BC.
同学甲说:要作辅助线;
同学乙说:要应用角平分线性质定理来解决:
同学丙说:要应用等腰三角形“三线合一”的性质定理来解决.
如果你是这个学习小组的成员,请你结合同学们的讨论写出证明过程.
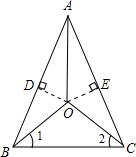 证明:如图,过O点作OD⊥AB于D,过O点作OE⊥AC于E.
证明:如图,过O点作OD⊥AB于D,过O点作OE⊥AC于E.∵OD⊥AB,OE⊥AC,AO平分∠BAC,
∴OD=OE.
∵∠1=∠2,
∴OB=OC.
在Rt△BDO和Rt△CEO中,
 ,
,∴△DOB≌△EOC(HL),
∴∠DBO=∠ECO,
∴∠ABC=∠ACB,
∴AB=AC.
∵OA平分∠BAC,
∴AO⊥BC.
分析:如图,过O点作OD⊥AB于D,过O点作OE⊥AC于E.利用角平分线的性质和全等三角形的判定定理HL证得Rt△DOB≌Rt△EOC(HL),则由全等三角形的性质和等角对等边得到
AB=AC,再利用等腰三角形“三线合一”的性质证得AO⊥BC.
点评:本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目