Question

在“课内比教学，课外访万家”活动中，某校规定所有老师必须进行讲课或说课比赛．九年级数学组参加决赛的A、B、C三位教师随机选择其中一种形式进行比赛．
（1）求三位教师同一种形式进行比赛的概率；
（2）求三位教师中至少有2人用讲课形式进行比赛的概率．

Answer 1

分析：（1）利用已知A、B、C三位教师故必须用树状图表示出所有的可能；
（2）利用树状图求出三位教师中至少有2人用讲课形式进行比赛的结果，进而求出概率即可．

解答：解：（1）画树状图

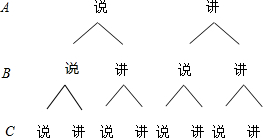
共有（说说说）、（说说讲）、（说讲说）、（说讲讲）、（讲说说）、（讲说讲）、（讲讲说）、（讲讲讲）8种结果，
其中同一种形式共有2种结果，所以其概率为P=

2

8

=

1

4

；

（2）由树状图可知，两人和两人以上用讲课形式比赛的结果有4种，
所以其概率P=

4

8

=

1

2

．

点评：此题主要考查了树状图法求概率，正确画出树状图得出所有可能是解题关键．