题目内容
设整数n满足0<n<1000,n=11×a,a也是整数,而且n的各位数字和恰好也是a,那么这样的n
- A.至少有3个
- B.恰有2个
- C.刚好有1个
- D.不存在
C
分析:根据整数n满足0<n<1000,则n是一个位数不多于3的一个整数,可以先设出这个数,然后根据整除性和各位上的数都是正整数,即可得到n的各位数的范围,从而求解.
解答:可设n= ,p,q,r是0~9中的数字.p,q,r不同时为0.
,p,q,r是0~9中的数字.p,q,r不同时为0.
又题意得n=100p+10q+r=11a=11(p+q+r),
89p=q+10r.
因q+10r≤99,
∴p只能取0或1.
若p=0.则只有q=r=0,n=0,引出矛盾.
故p=1,q=9,r=8,n=198.
故选C.
点评:本题主要考查了数的整除性,正确确定n的各个位上的数字之间的关系是解决本题的关键.
分析:根据整数n满足0<n<1000,则n是一个位数不多于3的一个整数,可以先设出这个数,然后根据整除性和各位上的数都是正整数,即可得到n的各位数的范围,从而求解.
解答:可设n=
 ,p,q,r是0~9中的数字.p,q,r不同时为0.
,p,q,r是0~9中的数字.p,q,r不同时为0.又题意得n=100p+10q+r=11a=11(p+q+r),
89p=q+10r.
因q+10r≤99,
∴p只能取0或1.
若p=0.则只有q=r=0,n=0,引出矛盾.
故p=1,q=9,r=8,n=198.
故选C.
点评:本题主要考查了数的整除性,正确确定n的各个位上的数字之间的关系是解决本题的关键.

练习册系列答案
相关题目
设整数n满足0<n<1000,n=11×a,a也是整数,而且n的各位数字和恰好也是a,那么这样的n( )
| A、至少有3个 | B、恰有2个 | C、刚好有1个 | D、不存在 |
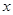 的方程
的方程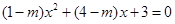 .
. 的取值范围;
的取值范围;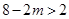 ,设二次函数
,设二次函数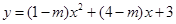 的图象与
的图象与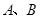 两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线
两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线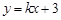 与此图象恰好有三个公共点时,求出
与此图象恰好有三个公共点时,求出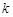 的值(只需要求出两个满足题意的k值即可).
的值(只需要求出两个满足题意的k值即可).
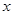 的方程
的方程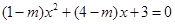 .
.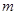 的取值范围;
的取值范围;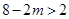 ,设二次函数
,设二次函数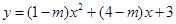 的图象与
的图象与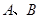 两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线
两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线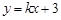 与此图象恰好有三个公共点时,求出
与此图象恰好有三个公共点时,求出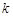 的值(只需要求出两个满足题意的k值即可).
的值(只需要求出两个满足题意的k值即可).