题目内容
【题目】已知AB∥CD.
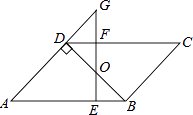
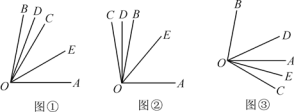
如图1,你能得出∠A+∠E+∠C=360°吗?
如图2,猜想出∠A.∠C、∠E的关系式并说明理由.
如图3,∠A.∠C、∠E的关系式又是什么?

【答案】图2中,∠A+∠C=∠E;图3中∠A+∠E-∠C=180°。
【解析】
过点E作AB的平行线EF,根据平行公理的推论得出EF∥CD,再根据平行线的性质进行推导,即可得出∠A、∠E、∠C之间的关系.
图1:过E作EF∥AB,如图所示:
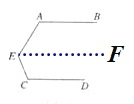
∴∠A+∠AEF=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴EF∥CD(平行公理的推论)
∴∠C+∠FEC=180°
结论:∠A+∠C+∠AEC=360°;
图2:过E作EF∥AB,如图所示:

∴EF//CD,∠BAE=∠AEF
∴∠FEC=∠DCE
∴∠A+∠C=∠FEC+∠AEF,即∠A+∠C=∠E.
图3:过E作EF∥AB,如图所示:
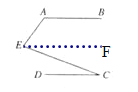
∴EF//CD,∠A+∠AEF=180°,
∴∠C=∠FEC,
∴∠A+∠FEC +∠AEF=180°+∠C, 即∠A+∠E-∠C=180°.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目