题目内容
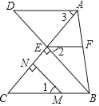
【题目】如图，过点
分别作
轴、
轴的平行线，交直线
于
、
两点，若反比例函数
的图象与
有公共点，则
的取值范围是（ ）
A.
B.
C.
D.
【答案】A
【解析】
由点C的坐标结合直线AB的解析式可得出点A、B的坐标，求出反比例函数图象过点C时的k值，将直线AB的解析式代入反比例函数解析式中，令其根的判别式△≥0可求出k的取值范围，取其最大值，找出此时交点的横坐标，进而可得出此点在线段AB上，综上即可得出结论．
解：令y＝x＋5中x＝1，则y＝4，
∴B（1，4）；
令y＝x＋5中y＝2，则x＝3，
∴A（3，2），
当反比例函数
（x＞0）的图象过点C时，有2＝
，
解得：k＝2，
将y＝x＋5代入中，整理得：x25x＋k＝0，
∵△＝（5）24k≥0，
∴k≤
，
当k＝时，解得：x＝
，
∵1＜＜3，
∴若反比例函数（x＞0）的图象与△ABC有公共点，则k的取值范围是2≤k≤，
故选：A．
练习册系列答案
相关题目
【题目】青少年“心理健康”问题已经引起了社会的关注，某中学对全校850名学生进行了一次“心理健康”知识测试，并从中抽取了50名学生的成绩（得分取正整数，满分为100分）作为样本，列出下面的频数分布表（单位：分）
成绩 | 50.5≤x＜60.5 | 60.5≤x＜70.5 | 70.5≤x＜80.5 | 80.5≤x＜90.5 | 90.5≤x＜100.5 |
频数 | 2 | 8 | 10 | 16 | 14 |
（1）组距是 ，组数是 ．
（2）成绩在60.5≤x＜80.5范围的频数是 ．
（3）画出频数分布直方图．
（4）若成绩在80分以上（不含80分）为优秀，试估计该校成绩优秀的有多少人？
