题目内容
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
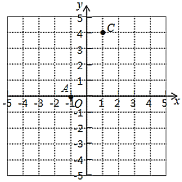
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形的面积为7?若存在,请直接写出点
三点为顶点的三角形的面积为7?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)B点的坐标为(2,0)或(-4,0);(2)6;(3)(0,![]() )或(0,-
)或(0,-![]() ).
).
【解析】
(1)根据A点的坐标和AB=3求出B点的坐标即可;
(2)根据点C的坐标和AB=3求出面积即可;
(3)先根据面积求出OP的长,再求出P点的坐标即可.
(1)∵A(-1,0),点B在x轴上,且AB=3,
∴-1+3=2,-1-3=-4,
∴B点的坐标为(2,0)或(-4,0);
(2)∵AB=3,C(1,4),A(-1,0),B点的坐标为(2,0)或(-4,0),
∴△ABC的面积为![]() ×3×4=6;
×3×4=6;
(3)在y轴上存在点P,使以A、B、P三点为顶点的三角形的面积为7,
理由是:∵AB=3,A、B在x轴上,P在y轴上,△ABP的面积为7,
∴![]() ×3×OP=7,
×3×OP=7,
解得:OP=![]() ,
,
根据对称性可知点P有两个,
故P点的坐标是(0,![]() )或(0,-
)或(0,-![]() ),
),
即在y轴上存在点P,使以A、B、P三点为顶点的三角形的面积为7,此时P点的坐标是(0,![]() )或(0,-
)或(0,-![]() ).
).

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目