题目内容
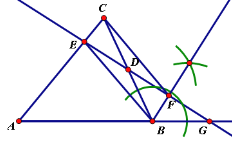
【题目】(8分)如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.

(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
【答案】(1)作图见解析;(2)证明见解析.
【解析】
试题(1)①作∠CBQ的平分线BP;②过点D作BP的垂线;
由BP//CE,可得∠ECD=∠FBD,∠CED=∠BFD,又CD=BD,从而△CDE≌△BDF,可得CE=BF,从而可得BF//CE,BF=CE,判定出四边形BFCE是平行四边形.
试题解析:(1)①作∠CBQ的平分线BP;②过点D作BP的垂线;
(2)∵BP//CE,∴∠ECD=∠FBD,∠CED=∠BFD,∵点D是BC的中点,∴CD=BD,∴△CDE≌△BDF,∴CE=BF,∵BF//CE,BF=CE,∴四边形BFCE是平行四边形.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目