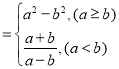题目内容
【题目】定义:若抛物线![]() 上有两点
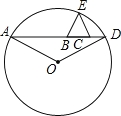
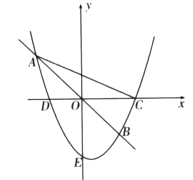
上有两点![]() 关于原点对称(点A在点B左侧)则称它为“完美抛物线”,如图.
关于原点对称(点A在点B左侧)则称它为“完美抛物线”,如图.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若抛物线![]() 是“完美抛物线”,求
是“完美抛物线”,求![]() 的值;
的值;
(3)若完美抛物线![]() 与
与![]() 轴交于点E与
轴交于点E与![]() 轴交于
轴交于![]() 两点(点D在点C的左侧),顶点为点
两点(点D在点C的左侧),顶点为点![]() ,
,![]() 是以
是以![]() 为直角边的直角三角形,点
为直角边的直角三角形,点![]() ,求点
,求点![]() 中
中![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)-2
;(3)-2
【解析】
(1)根据点![]() ,
,![]() 关于原点对称,得到B点坐标,再代入二次函数即可求出b的值;
关于原点对称,得到B点坐标,再代入二次函数即可求出b的值;
(2)设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,代入二次函数得到
,代入二次函数得到![]() ,再根据
,再根据![]() ,可知点B的坐标为
,可知点B的坐标为![]() ,
,![]() 在直线
在直线![]() 上,利用
上,利用![]() 即可求出
即可求出![]() ;
;
(3)根据![]() 是以
是以![]() 为直角边的直角三角形,得到
为直角边的直角三角形,得到![]() ,再求出点C的坐标为
,再求出点C的坐标为![]() ,代入二次函数得
,代入二次函数得![]() ,把
,把![]() 代入③得
代入③得![]() ,故
,故![]() ,然后得到
,然后得到![]() ,故可求出ac的值.
,故可求出ac的值.
解:(1)由题意得,因为点![]() ,
,![]() 关于原点对称,点
关于原点对称,点![]() ,
,
∴![]()
将![]() ,
,![]() 代入
代入![]()
得![]()
解得![]() ,
,
(2)设点![]() 的坐标为
的坐标为![]()
则点![]() 的坐标为
的坐标为![]()
因为点![]() 在抛物线上,把A,B代入
在抛物线上,把A,B代入![]()
∴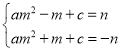
解得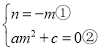
因为![]() 关于原点对称,所以
关于原点对称,所以![]() 三点共线,
三点共线, ![]() ,
,
![]() ,
,![]()
点B的坐标为![]()
所以![]() 在直线
在直线![]() 上
上
![]() ;
;
(3)因为![]() 是以
是以![]() 为直角边的直角三角形
为直角边的直角三角形
![]()
所以点C的坐标为![]()
![]() ③
③
把②代入③得![]()
![]()
将![]() 代入
代入![]() ,
,![]()
![]() .
.

【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
【题目】小明用礼花发射器发射彩纸礼花,每隔1.6秒发射一花弹,每束花弹发射的飞行路径,花弹爆炸的高度均相同,小明发射的第一束花弹的飞行高度![]() 米与飞行时间
米与飞行时间![]() 秒变化的规律如下表:
秒变化的规律如下表:
| 0 | 0.5 | 1 | 2 | 2.5 | 3 | …… |
| 1.5 |
| 2.75 | 3.5 |
| 3.75 | …… |
(1)根据表格中的数据选择适当的函数来表示![]() 与
与![]() 之间的关系,求出相应的函数解析式;
之间的关系,求出相应的函数解析式;
(2)当![]() 时,第一花束飞行到最高点,此时的高度为
时,第一花束飞行到最高点,此时的高度为![]() ,在
,在![]() 的情况下,求
的情况下,求![]() 的表达式,并判断这个表达式的变化趋势,若有变化,请说明变化过程,若是定值请求出这个定值;
的表达式,并判断这个表达式的变化趋势,若有变化,请说明变化过程,若是定值请求出这个定值;
(3)为了安全,要求花弹爆炸的高度不低于3米,小明发现在第一束花弹爆炸的同时,第三束花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求?