题目内容
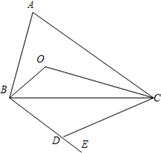20、如图，∠A=75°，∠BOC=135°，∠ABO=∠CBE，∠ACO=∠BCD，则∠CDE=60°
．分析：由∠BOC=135°和内角和定理求出∠OBC与∠OCB的和，然后求出∠ABO与∠ACO和，所以∠CDE=∠CBE+∠BCD=∠ABO+∠ACO．
解答：解：∵∠BOC=135°，
∴∠OBC+∠OCB=180°-135°=45°，
∵∠ABO+∠ACO=180°-∠A-45°=60°，
∴CDE=∠CBE+∠BCD=∠ABO+∠ACO=60°．
故答案为60°．
∴∠OBC+∠OCB=180°-135°=45°，
∵∠ABO+∠ACO=180°-∠A-45°=60°，
∴CDE=∠CBE+∠BCD=∠ABO+∠ACO=60°．
故答案为60°．
点评：本题主要考查了三角形内角和定理和三角形外角的性质，解答的关键是沟通外角和内角的关系，难度适中．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
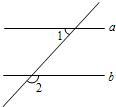2、如图，∠1=75°，要使a∥b，则∠2等于（ ）
如图，∠A=75°，则∠BOC=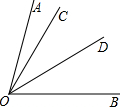
已知：如图，∠AOB=75°，∠AOC=15°，OD是∠BOC的平分线，求∠BOD的度数．