题目内容
8、如图,∠1=75°,∠A=∠BCA,∠CBD=∠CDB,∠DCE=∠DEC,∠EDF=∠EFD.则∠A的度数为( )


分析:首先假设∠A=x,利利用外角知识,表示出∠A=∠BCA=x,∠CBD=∠CDB=2x,∠DCE=∠DEC=3x,∠EDF=∠EFD=4x,进而求出∠A的度数.
解答: 解:∵∠A=∠BCA,∠CBD=∠CDB,∠DCE=∠DEC,∠EDF=∠EFD,
解:∵∠A=∠BCA,∠CBD=∠CDB,∠DCE=∠DEC,∠EDF=∠EFD,
∴设∠A=x,
∴∠A=∠BCA=x,∠CBD=∠CDB=2x,∠DCE=∠DEC=3x,∠EDF=∠EFD=4x,
∠1=180°-3x-(180°-8x)=75°,
∠1=5x=75°,
∴x=15°,
即:∠A=15°.
故选A.
 解:∵∠A=∠BCA,∠CBD=∠CDB,∠DCE=∠DEC,∠EDF=∠EFD,
解:∵∠A=∠BCA,∠CBD=∠CDB,∠DCE=∠DEC,∠EDF=∠EFD,∴设∠A=x,
∴∠A=∠BCA=x,∠CBD=∠CDB=2x,∠DCE=∠DEC=3x,∠EDF=∠EFD=4x,
∠1=180°-3x-(180°-8x)=75°,
∠1=5x=75°,
∴x=15°,
即:∠A=15°.
故选A.
点评:此题主要考查了三角形外角的性质,利用∠A=x得出各角含有x式子,是解决问题的关键.

练习册系列答案
相关题目
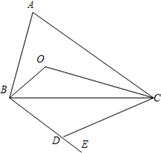 20、如图,∠A=75°,∠BOC=135°,∠ABO=∠CBE,∠ACO=∠BCD,则∠CDE=
20、如图,∠A=75°,∠BOC=135°,∠ABO=∠CBE,∠ACO=∠BCD,则∠CDE=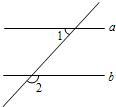 2、如图,∠1=75°,要使a∥b,则∠2等于( )
2、如图,∠1=75°,要使a∥b,则∠2等于( ) 如图,∠A=75°,则∠BOC=
如图,∠A=75°,则∠BOC=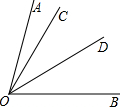 已知:如图,∠AOB=75°,∠AOC=15°,OD是∠BOC的平分线,求∠BOD的度数.
已知:如图,∠AOB=75°,∠AOC=15°,OD是∠BOC的平分线,求∠BOD的度数.