题目内容
 如图,A、B、C为双曲线
如图,A、B、C为双曲线 (x>0)上的三点,过A、B、C分别作两坐标轴的垂线与两坐标轴围成的三个矩形从左至右面积依次记为s1、s2、s3,则s1、s2、s3之间的大小关系为
(x>0)上的三点,过A、B、C分别作两坐标轴的垂线与两坐标轴围成的三个矩形从左至右面积依次记为s1、s2、s3,则s1、s2、s3之间的大小关系为
- A.s1>s2>s3
- B.s2>s3>s1
- C.s3>s2>s1
- D.s1=s2=s3
D
分析:根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系S= |k|即可判断.
|k|即可判断.
解答:因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,
即S= |k|,所以S1=S2=S3.
|k|,所以S1=S2=S3.
故选D.
点评:主要考查了反比例函数 中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|.
|k|.
分析:根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系S=
 |k|即可判断.
|k|即可判断.解答:因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,
即S=
 |k|,所以S1=S2=S3.
|k|,所以S1=S2=S3.故选D.
点评:主要考查了反比例函数
 中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|.
|k|. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,隧道的截面是抛物线,可以用y=-
如图,隧道的截面是抛物线,可以用y=-| 1 |
| 16 |
| A、不大于4m |
| B、恰好4m |
| C、不小于4m |
| D、大于4m,小于8m |
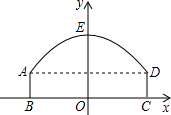 线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.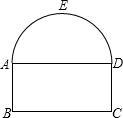 如图,隧道的截面由圆弧AED和矩形ABCD构成,矩形的长BC为12m,宽AB为3m,隧道的顶端E(圆弧AED的中点)高出道路(BC)7m.
如图,隧道的截面由圆弧AED和矩形ABCD构成,矩形的长BC为12m,宽AB为3m,隧道的顶端E(圆弧AED的中点)高出道路(BC)7m.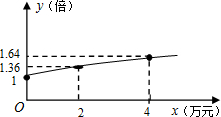 ,设每双鞋的成本价为a元.
,设每双鞋的成本价为a元.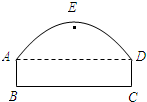 如图,某隧道的截面由抛物线AED和矩形ABCD构成,整个图形是轴对称图形.矩形的长BC为8m,宽AB为2m,抛物线的顶点E到地面距离为6m.
如图,某隧道的截面由抛物线AED和矩形ABCD构成,整个图形是轴对称图形.矩形的长BC为8m,宽AB为2m,抛物线的顶点E到地面距离为6m.