题目内容
【题目】如图,在平行四边形ABCD中,AB=2AD,BE平分∠ABC交CD于点E,作BF⊥AD,垂足为F,连接EF,小明得到三个结论:①∠FBC=90°;②ED=EB;③S△EBF=S△EDF+S△EBC;则三个结论中一定成立的是_____.
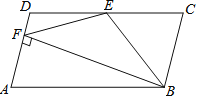
【答案】①③
【解析】
由垂直的定义得到∠AFB=90°,根据平行线的性质即可得到∠AFB=∠CBF=90°,故①正确;延长FE交BC的延长线与M,根据全等三角形的性质得到EF=EM=![]() FM,根据直角三角形的性质得到BE=
FM,根据直角三角形的性质得到BE=![]() FM,等量代换的EF=BE,故②错误;由于S△BEF=S△BME,S△DFE=S△CME,于是得到S△EBF=S△BME=S△EDF+S△EBC.故③正确.
FM,等量代换的EF=BE,故②错误;由于S△BEF=S△BME,S△DFE=S△CME,于是得到S△EBF=S△BME=S△EDF+S△EBC.故③正确.
解:∵BF⊥AD,
∴∠AFB=90°,
∵在平行四边形ABCD中,AD∥BC,
∴∠AFB=∠CBF=90°,故①正确;
延长FE交BC的延长线与M,

∴∠DFE=∠M,
在△DFE与△CME中,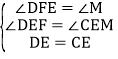 ,
,
∴△DFE≌△CME(AAS),
∴EF=EM=![]() FM,
FM,
∵∠FBM=90°,
∴BE=![]() FM,
FM,
∴EF=BE,
∵EF≠DE,
故②错误;
∵EF=EM,
∴S△BEF=S△BME,
∵△DFE≌△CME,
∴S△DFE=S△CME,
∴S△EBF=S△BME=S△EDF+S△EBC.故③正确.
故答案为:①③.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目