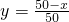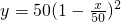题目内容
一个容器内盛满纯酒精50kg，第一次倒出若干千克纯酒精后加入同千克的水；第二次又倒出相同千克的酒精溶液，这时容器内酒精溶液含纯酒精ykg，设每次倒出的xkg，则y与x之间的函数关系式为（ ）
| A、y=50（50-x） | ||
B、y=
| ||
| C、y=（50-x）2 | ||
D、y=50(1-
|
分析：先求出加水后酒精浓度=
，然后根据酒精质量=溶液质量×酒精浓度可得出答案．
| 50-x |
| 50 |
解答：解：加水后酒精浓度=
，第二次倒出后容器内剩余的质量为：（50-x）kg，
故剩余的酒精=（50-x）×
=50（1-
）2，
故选D．
| 50-x |
| 50 |
故剩余的酒精=（50-x）×
| 50-x |
| 50 |
| x |
| 50 |
故选D．
点评：本题考查了根据实际问题抽象二次函数关系式的知识，求出酒精浓度及剩余的溶液质量是解答本题的关键．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
，问第一次倒出酒精多少升？
