Question

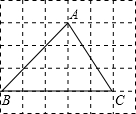（2013•江都市二模）如图，A、B、C三点在正方形网格线的交点处，则tan∠BAC的值为

5

．

Answer 1

分析：过点C作CD⊥AB于点D，则可判断△DBC是等腰直角三角形，求出BD，可得出AD，再由△ABC面积的两种表示方法，可求出CD，继而求出tan∠BAC的值．

解答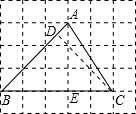：解：由格点三角形，可得∠ABC=45°，AB=

32+32

=3

2

，
过点C作CD⊥AB于点D，则△DBC是等腰三角形，
∵BC=5，
∴BD=

5 2

2

，
∴CD=BD=

5 2

2

，
∴tan∠BAC=

DC

AD

=5．
故答案为：5．

点评：本题考查了勾股定理的知识，解答本题的关键是作出辅助线，求出CD、AD的长度，注意在格点三角形中应用勾股定理．