题目内容
设p,q都是实数,且 .我们规定:满足不等式
.我们规定:满足不等式 的实数x的所有取值的全体叫做闭区间,表示为
的实数x的所有取值的全体叫做闭区间,表示为 .对于一个函数,如果它的自变量x与函数值y满足:当
.对于一个函数,如果它的自变量x与函数值y满足:当 时,有
时,有 ,我们就称此函数是闭区间
,我们就称此函数是闭区间 上的“闭函数”.
上的“闭函数”.
(1)反比例函数 是闭区间
是闭区间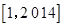 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间
是闭区间 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;
(3)若实数c,d满足 ,且
,且 ,当二次函数
,当二次函数 是闭区间
是闭区间 上的“闭函数”时,求c,d的值.
上的“闭函数”时,求c,d的值.
(1)是,理由见解析;(2) 或
或 ;(3)
;(3) ,
, .
.
解析试题分析:(1)根据反比例函数 的单调区间进行判断.
的单调区间进行判断.
(2)根据新定义运算法则列出关于系数k、b的方程组 或
或 ,通过解该方程组即可求得系数k、b的值.
,通过解该方程组即可求得系数k、b的值.
(3)由于函数 的图象开口向上,且对称轴为
的图象开口向上,且对称轴为 ,顶点为
,顶点为 ,由题意根据图象,分
,由题意根据图象,分 和
和 两种情况讨论即可.
两种情况讨论即可.
试题解析:(1)是. 由函数 的图象可知,当
的图象可知,当 时,函数值y随着自变量x的增大而减少,而当
时,函数值y随着自变量x的增大而减少,而当 时,
时, ;
; 时,
时, ,故也有
,故也有 ,
,
所以,函数 是闭区间
是闭区间 上的“闭函数”.
上的“闭函数”.
(2)因为一次函数 是闭区间
是闭区间 上的“闭函数”,所以根据一次函数的图象与性质,必有:
上的“闭函数”,所以根据一次函数的图象与性质,必有:
①当 时,
时, ,解之得
,解之得 .
.
∴一次函数的解析式为 .
.
②当 时,
时, ,解之得
,解之得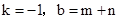 .
.
∴一次函数的解析式为 .
.
故一次函数的解析式为 或
或 .
.
(3)由于函数 的图象开口向上,且对称轴为
的图象开口向上,且对称轴为 ,顶点为
,顶点为 ,由题意根据图象,分以下两种情况讨论:
,由题意根据图象,分以下两种情况讨论:
①当 时,必有
时,必有 时,
时,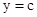 且
且 时,
时, ,
,
即方程 必有两个不等实数根,解得
必有两个不等实数根,解得 .
.
而0,6分布在2的两边,这与 矛盾,舍去;
矛盾,舍去;
②当 时,必有函数值y的最小值为
时,必有函数值y的最小值为 ,
,
由于此二次函数是闭区间 上的“闭函数”,故必有
上的“闭函数”,故必有 ,从而有
,从而有 .
.
而当 时,
时, ,即得点
,即得点 ;
;
又点 关于对称轴
关于对称轴 的对称点为
的对称点为 ,
,
由“闭函数”的定义可知必有 时,
时, ,即
,即 ,解得
,解得 .
.
故可得 ,
, 符合题意.
符合题意.
综上所述, ,
, 为所求的实数.
为所求的实数.
考点:1.新定义;2.反比例函数、一次函数和二次函数的性质;3.解二元方程组;4.分类思想的应用.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案 与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.

 2
2 图象上,求这两个函数图象的另一交点N的坐标.
图象上,求这两个函数图象的另一交点N的坐标. 
 ?若存在,求出t的值;若不存在,请说明理由.
?若存在,求出t的值;若不存在,请说明理由.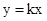 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标; ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
 的图象的一个交点为A(2, m).
的图象的一个交点为A(2, m). (
( )与一次函数
)与一次函数 (
( )相交于A、B两点,AC⊥
)相交于A、B两点,AC⊥ 轴于点C.若△OAC的面积为1,且tan∠AOC=2.
轴于点C.若△OAC的面积为1,且tan∠AOC=2. 的值大于一次函数
的值大于一次函数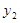 的值?
的值?
 (个)与甲品牌文具盒数量
(个)与甲品牌文具盒数量 (个)之间的函数关系如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7 200元.
(个)之间的函数关系如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7 200元.