题目内容
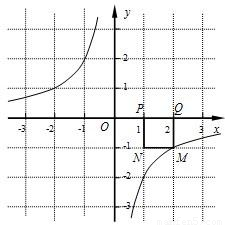
(2010•金华)已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-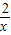 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.(1)如图所示,若反比例函数解析式为y=-
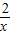 ,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是______.
,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是______.(2)请你通过改变P点坐标,对直线M1M的解析式y﹦kx+b进行探究可得k﹦______,若点P的坐标为(m,0)时,则b﹦______;
(3)依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标.
【答案】分析:(1)根据要求,画出符合条件的另一个正方形PQ1M1N1,即可写出点M1的坐标;
(2)由于四边形PQMN与四边形PQ1M1N1都是正方形,结合图象分析,可得出M1、P、M三点共线,再求得直线M1M的斜率,代入P点坐标,求得b=m;
(3)依据(2)的规律,如果点P的坐标为(6,0),则直线M1M的解析式为y=-x+6,又点M(x,y)在反比例函数y=- 的图象上,故x•(-x+6)=-2,解此方程,求出x的值,进而得出点M1和点M的坐标.
的图象上,故x•(-x+6)=-2,解此方程,求出x的值,进而得出点M1和点M的坐标.
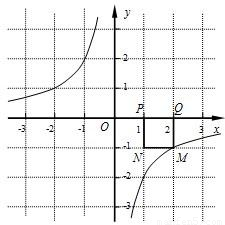
解答:解:(1)如图,画出符合条件的另一个正方形PQ1M1N1,
则容易看出M1的坐标为(-1,2);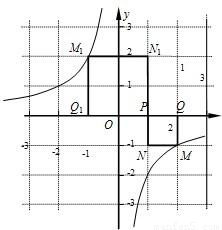
(2)由于四边形PQMN与四边形PQ1M1N1都是正方形,
则∠MPN=∠Q1PM1=45°,∠Q1PN=90°,∴∠M1PM=180°,
∴M1、P、M三点共线,由tan∠Q1PM1=1,
可知不管P点在哪里,k﹦-1;
把x=m代入y=-x+b,得b=m;
(3)由(2)知,直线M1M的解析式为y=-x+6,
则M(x,y)满足x•(-x+6)=-2,
解得x1=3+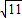 ,x2=3-
,x2=3- ,
,
∴y1=3-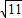 ,y2=3+
,y2=3+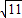 .
.
∴M1,M的坐标分别为(3-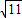 ,3+
,3+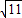 ),(3+
),(3+ ,3-
,3-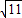 ).
).
点评:此题综合考查了反比例函数的性质,正方形等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.
(2)由于四边形PQMN与四边形PQ1M1N1都是正方形,结合图象分析,可得出M1、P、M三点共线,再求得直线M1M的斜率,代入P点坐标,求得b=m;
(3)依据(2)的规律,如果点P的坐标为(6,0),则直线M1M的解析式为y=-x+6,又点M(x,y)在反比例函数y=-
 的图象上,故x•(-x+6)=-2,解此方程,求出x的值,进而得出点M1和点M的坐标.
的图象上,故x•(-x+6)=-2,解此方程,求出x的值,进而得出点M1和点M的坐标.解答:解:(1)如图,画出符合条件的另一个正方形PQ1M1N1,
则容易看出M1的坐标为(-1,2);

(2)由于四边形PQMN与四边形PQ1M1N1都是正方形,
则∠MPN=∠Q1PM1=45°,∠Q1PN=90°,∴∠M1PM=180°,
∴M1、P、M三点共线,由tan∠Q1PM1=1,
可知不管P点在哪里,k﹦-1;
把x=m代入y=-x+b,得b=m;
(3)由(2)知,直线M1M的解析式为y=-x+6,
则M(x,y)满足x•(-x+6)=-2,
解得x1=3+
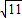 ,x2=3-
,x2=3- ,
,∴y1=3-
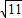 ,y2=3+
,y2=3+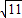 .
.∴M1,M的坐标分别为(3-
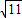 ,3+
,3+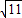 ),(3+
),(3+ ,3-
,3-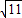 ).
).点评:此题综合考查了反比例函数的性质,正方形等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.

练习册系列答案
相关题目
 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.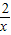 ,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是______.
,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是______.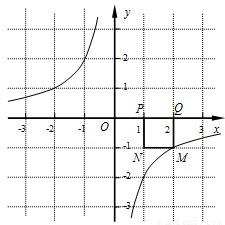
 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.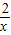 ,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是______.
,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是______.