题目内容
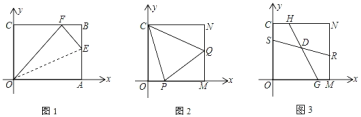
【题目】如图,在边长为 2 的正方形 ABCD 中剪去一个边长为 1 的小正方形 EFGD ,动点 P 从点 A 出发,沿A E F G C B 的路线,绕多边形的边匀速运动到点 B 时停止,则 ABP 的面积 S 随着时间t 变化的函数图象大致是( )

A. B.
B. C.
C. D.
D.
【答案】A
【解析】
根据点P在AE、EF、FG、GC、CB上时,△ABP的面积S与时间t的关系确定函数图象.
当点P在AE上时,△ABP的底不变,高增大,所以△ABP的面积S随着时间t的增大而增大;
当点P在EF上时,△ABP的底不变,高不变,所以△ABP的面积S不变;
当点P在FG上时,△ABP的底不变,高增大,所以△ABP的面积S随着时间t的增大而增大;
当点P在GC上时,△ABP的底不变,高不变,所以△ABP的面积S不变;
当点P在CB上时,△ABP的底不变,高减小,所以△ABP的面积S随着时间t的增大而减小;
故答案为:A.

练习册系列答案
相关题目