题目内容
如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM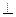 BE,垂足为M,AM交BD于点F.
BE,垂足为M,AM交BD于点F.
(1)求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM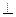 BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

(1)证明:∵四边形ABCD是正方形.
∴ BOE=
BOE= AOF=90
AOF=90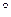 .OB=OA ……………… (1分)
.OB=OA ……………… (1分)
又∵AM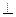 BE,∴
BE,∴ MEA+
MEA+ MAE=90
MAE=90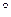 =
= AFO+
AFO+ MAE
MAE
∴ MEA=
MEA= AFO………………(2分)
AFO………………(2分)
∴Rt△BOE≌ Rt△AOF ……………… (3分)
∴OE="OF " ………………(4分)
(2)OE=OF成立 ……………… (5分)
证明:∵四边形ABCD是正方形,
∴ BOE=
BOE= AOF=90
AOF=90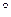 .OB=OA ……………… (6分)
.OB=OA ……………… (6分)
又∵AM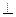 BE,∴
BE,∴ F+
F+ MBF=90
MBF=90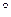 =
= B+
B+ OBE
OBE
又∵ MBF=
MBF= OBE
OBE
∴ F=
F= E………………(7分)
E………………(7分)
∴Rt△BOE≌ Rt△AOF ……………… (8分)
∴OE="OF " ………………(9分)
解析

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目




 如图1,已知正方形OABC的边长为4,等腰直角三角板OEF的直角边OE、OF分别在OA、OC上,且OE=2.将三角板OEF绕点O逆时针旋转至OE1F1的位置,旋转角为α,连接CF1、AE1.
如图1,已知正方形OABC的边长为4,等腰直角三角板OEF的直角边OE、OF分别在OA、OC上,且OE=2.将三角板OEF绕点O逆时针旋转至OE1F1的位置,旋转角为α,连接CF1、AE1.