Question

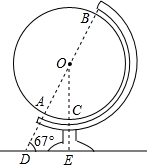如图，点A、B为地球仪的南、北极点，直线AB与放置地球仪的平面交于点D，所成的角度约为67°，半径OC所在的直线与放置平面垂直，垂足为点E．DE=15cm，AD=14cm．求半径OA的长．（精确到0.1cm） （参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）

Answer 1

分析：在Rt△ODE中，DE=15，∠ODE=67°，根据∠ODE的余弦值，即可求得OD长，减去AD即为OA．

解答：解：在Rt△ODE中，DE=15，∠ODE=67°，
∵cos∠ODE=

DE

DO

，
∴OD≈

15

0.39

≈38.46（cm），
∴OA=OD-AD≈38.46-14≈24.5（cm）．
答：半径OA的长约为24.5cm．

点评：此题主要考查了解直角三角形的应用，本题把实际问题转化成数学问题，利用三角函数中余弦定义来解题是解题关键．