题目内容
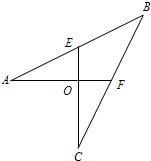22、如图，AF⊥CE，垂足为点O，AO=CO=2，EO=FO=1．（1）求证：点F为BC的中点；
（2）求四边形BEOF的面积．
分析：（1）解题思路：连接EF、AC，可通过证明EF是三角形ABC的中位线来求得；
（2）连接OB后我们发现，S△OFC=S△FOB，S△OEB=S△OEA，那么S四边形BEOF=S△OEA+S△OFC．
（2）连接OB后我们发现，S△OFC=S△FOB，S△OEB=S△OEA，那么S四边形BEOF=S△OEA+S△OFC．
解答：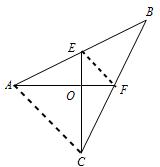
证明：（1）连接EF、AC
∵AO=CO=2，EO=FO=1
∴EO：OC=FO：OA=1：2
又∵∠EOF=∠AOC
∴△AOC∽△FOE
∴EF：AC=1：2，∠OEF=∠OCA
∴EF∥AC
∴EF是三角形ABC的中位线
∴点F为BC的中点；
（2）连接OB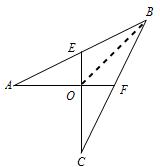
由（1）知：BF=CF
又因为△OFC和△BFO中CF和BF边上的高相等，那么
S△OFC=S△BFO
同理：S△BOE=S△AOE
直角三角形AOE中，S△AOE=1×2÷2=1
同理S△OFC=1
因此S四边形BEOF=S△BFO+S△BOE=S△OFC+S△AOE=2．
证明：（1）连接EF、AC∵AO=CO=2，EO=FO=1
∴EO：OC=FO：OA=1：2
又∵∠EOF=∠AOC
∴△AOC∽△FOE
∴EF：AC=1：2，∠OEF=∠OCA
∴EF∥AC
∴EF是三角形ABC的中位线
∴点F为BC的中点；
（2）连接OB
由（1）知：BF=CF
又因为△OFC和△BFO中CF和BF边上的高相等，那么
S△OFC=S△BFO
同理：S△BOE=S△AOE
直角三角形AOE中，S△AOE=1×2÷2=1
同理S△OFC=1
因此S四边形BEOF=S△BFO+S△BOE=S△OFC+S△AOE=2．
点评：本题考查的是相似多边形的判定和性质，三角形中位线定理的逆定理，三角形的面积公式等知识点．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
上一动点，AK、DC的延长线相交于点F，连接CK、KD．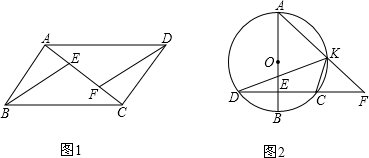
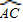上一动点，AK、DC的延长线相交于点F，连接CK、KD．
