题目内容
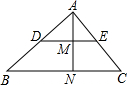 已知:点D、E分别为△ABC的边AB、AC上的中点,AN⊥BC,交DE于点M,则AM:AN的值为
已知:点D、E分别为△ABC的边AB、AC上的中点,AN⊥BC,交DE于点M,则AM:AN的值为1:2
1:2
.分析:利用三角形中位线定理推知DE∥BC,且DE=
BC.则△ADE∽△ABC,所以根据相似三角形对应边上的高之比等于相似比求解.
| 1 |
| 2 |
解答:解:如图,∵点D、E分别为△ABC的边AB、AC上的中点,
∴DE∥BC,且DE=
BC.
∴△ADE∽△ABC,
∴AM:AN=DE:BC=1:2.
故答案是:1:2.
∴DE∥BC,且DE=
| 1 |
| 2 |
∴△ADE∽△ABC,
∴AM:AN=DE:BC=1:2.
故答案是:1:2.
点评:本题考查了相似三角形的判定与性质、三角形中位线定理.三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
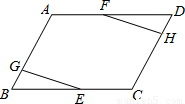
 已知:点E、F分别为?ABCD的边BC、DA的中点,EG⊥AB,FH⊥DC,垂足为G、H.
已知:点E、F分别为?ABCD的边BC、DA的中点,EG⊥AB,FH⊥DC,垂足为G、H.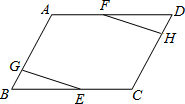 已知:点E、F分别为?ABCD的边BC、DA的中点,EG⊥AB,FH⊥DC,垂足为G、H.
已知:点E、F分别为?ABCD的边BC、DA的中点,EG⊥AB,FH⊥DC,垂足为G、H.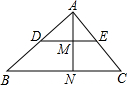 已知:点D、E分别为△ABC的边AB、AC上的中点,AN⊥BC,交DE于点M,则AM:AN的值为________.
已知:点D、E分别为△ABC的边AB、AC上的中点,AN⊥BC,交DE于点M,则AM:AN的值为________.