题目内容
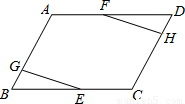
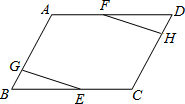 已知:点E、F分别为?ABCD的边BC、DA的中点,EG⊥AB,FH⊥DC,垂足为G、H.
已知:点E、F分别为?ABCD的边BC、DA的中点,EG⊥AB,FH⊥DC,垂足为G、H.
求证:EG=FH.
证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,
∵F为AD中点,E为BC中点,
∴DF= AD,BE=
AD,BE= BC,
BC,
∴DF=BE,
∵EG⊥AB,FH⊥DC,
∴∠FHD=∠EGB=90°,
∵在△BGE和△DHF中
 ,
,
∴△BGE≌△DHF(AAS),
∴EG=FH.
分析:根据平行四边形性质求出∠B=∠D,AD=BC,求出DF=BE,∠FHD=∠EGB=90°,根据AAS证△BGE≌△DHF,即可得出答案.
点评:本题考查了平行四边形的性质,全等三角形的性质和判定,垂直定义等知识点,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
∴∠B=∠D,AD=BC,
∵F为AD中点,E为BC中点,
∴DF=
 AD,BE=
AD,BE= BC,
BC,∴DF=BE,
∵EG⊥AB,FH⊥DC,
∴∠FHD=∠EGB=90°,
∵在△BGE和△DHF中
 ,
,∴△BGE≌△DHF(AAS),
∴EG=FH.
分析:根据平行四边形性质求出∠B=∠D,AD=BC,求出DF=BE,∠FHD=∠EGB=90°,根据AAS证△BGE≌△DHF,即可得出答案.
点评:本题考查了平行四边形的性质,全等三角形的性质和判定,垂直定义等知识点,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
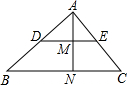 已知:点D、E分别为△ABC的边AB、AC上的中点,AN⊥BC,交DE于点M,则AM:AN的值为
已知:点D、E分别为△ABC的边AB、AC上的中点,AN⊥BC,交DE于点M,则AM:AN的值为 已知:点E、F分别为?ABCD的边BC、DA的中点,EG⊥AB,FH⊥DC,垂足为G、H.
已知:点E、F分别为?ABCD的边BC、DA的中点,EG⊥AB,FH⊥DC,垂足为G、H.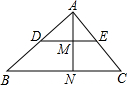 已知:点D、E分别为△ABC的边AB、AC上的中点,AN⊥BC,交DE于点M,则AM:AN的值为________.
已知:点D、E分别为△ABC的边AB、AC上的中点,AN⊥BC,交DE于点M,则AM:AN的值为________.