题目内容
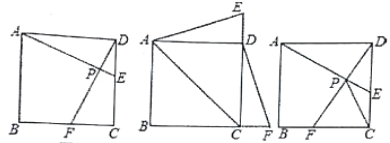
【题目】如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.
(1)求证:∠P=90°﹣![]() ∠C;
∠C;
(2)当∠C=90°,ND=NP时,判断线段MP与AM的数量关系,并给予证明.
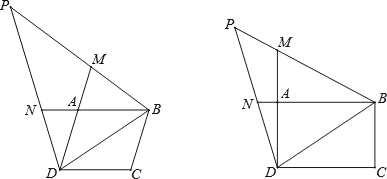
【答案】(1)证明见解析;(2)![]()
【解析】分析(1)首先过点B作BF⊥PD于点F,过点D作DG⊥BP于点G,BF与DG交于点H,由BD=BN=DM,可得BF与DG是∠DBN、∠MDB的平分线,又由四边形内角和为360°,可得∠P+∠FHG=180°,继而可得∠DHB=∠FHG=180°-∠P=90°+![]() ∠C,则可证得结论;
∠C,则可证得结论;
(2)首先过点P作PS⊥CD于点S,PR⊥BC于点R,易证得△PKD≌△PSD(AAS),同理:△PKB≌△PRB,然后延长BN交QS于点Q,则Q为PS的中点,设QS=PQ=x,即可求得答案.
详解(1)证明:过点B作BF⊥PD于点F,过点D作DG⊥BP于点G,BF与DG交于点H,
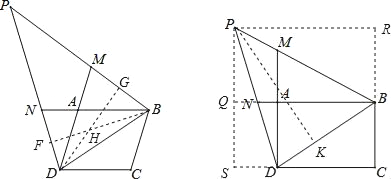
∴∠FHG+∠P=180°,
∴∠DHB+∠P=180°,
∴∠DHB=180°﹣∠P,
∵BD=BN=DM,
∴BF与DG是∠DBN、∠MDB的平分线,
∴由四边形内角和为360°,可得∠P+∠FHG=180°,
∵∠DHB=180°﹣(∠GDB+∠FBD)=180°﹣![]() (180°﹣∠DAB)=90°﹣
(180°﹣∠DAB)=90°﹣![]() ∠DAB,
∠DAB,
∵四边形ABCD是平行四边形,
∴∠DAB=∠C,
∴∠DHB=90°﹣![]() ∠C,
∠C,
∵∠DHB=180°﹣∠P,
∴180°﹣∠P=90°+![]() ∠C,
∠C,
∴∠P=90°﹣![]() ∠C;
∠C;
(2)MP:AM=![]() :2.
:2.
理由:过点P作PS⊥CD于点S,PR⊥BC于点R,
当∠C=90°时,则∠DPB=45°,
∵BN∥CD,
∴∠BND=∠BDN=∠SDN,
同理:∠PBD=∠PBR,
作PK⊥BD于点K,
在△PKD和△PSD中,
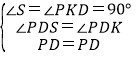
∴△PKD≌△PSD(AAS),
同理:△PKB≌△PRB,
∴PS=PR,
∴四边形PSCR是正方形,
延长BN交QS于点Q,则Q为PS的中点,
设QS=PQ=x,
则PS=CS=RC=2x,RB=KB=x,
设SD=m,BD=x+m,
则(x+m)2=x2+(2x﹣m)2,
∴m:x=2:3,
∴DK=SD=![]() x,BD=
x,BD=![]() x,
x,
∴AM=DM﹣AD=BD﹣AD=![]() x,
x,
根据勾股定理得,AB=![]() =
=![]() x,
x,
在Rt△ABM中,BM=![]() ,
,
∴PB=![]() ,
,
∴PM=![]() ,
,
∴MP:AM=![]() :2.
:2.