Question

已知：一元二次方程x²+px+q+1=0的一根为2．
（1）求q关于p的关系式；
（2）求证：抛物线y=x²+px+q+1与x轴总有交点；
（3）当p=-1时，（2）中的抛物线与x轴交于A、B两点，与y轴交于C点，A在B的左侧，若P点在抛物线上，当S_△BPC=4时，求P点的坐标．

Answer 1

（1）解：∵方程的根为2，
∴4+2p+q+1=0，
∴q=-2p-5；

（2）证明：△=p²-4（q+1），
=p²-4（-2p-5+1），
=p²+8p+16，
=（p+4）²，
∵（p+4）²≥0，
∴△≥0，
∴抛物线y=x²+px+q+1与x轴总有交点；

（3）解：当p=-1时，q=-2×（-1）-5=-3，
∴抛物线的解析式为：y=x²-x-2．
∵B（2，0）C（0，-2），
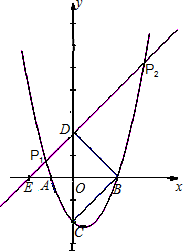
∴BC=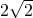，∠OBC=45°．
∵S_△PBC=4．
∴．
∴．
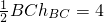过B点作BD⊥BC交y轴于点D，
∴DO=BO=CO，
∴D点的坐标为：（0，2），
∴BD=，
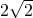过D点作DE∥BC交x轴于点E，
∵∠ODB=∠OBD=45°∠EDB=90°，
∴∠EDO=45°，
∴E（-2，0），
设直线DE的解析式为y=kx+b（k≠0），
∴，
∴解得，
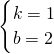∴直线DE的解析式为y=x+2．
设直线DE与抛物线的交点P（x，y），
∴，
∴，
∴，．
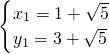
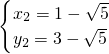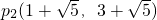分析：（1）将2代替一元二次方程x²+px+q+1=0中的x即可得到pq之间的关系式；
（2）证明抛物线与x轴总有交点即可证明其根的判别式中大于零即可；
（3）利用p=-1求得抛物线的解析式，利用围成的三角形的面积求得P点的坐标即可．
点评：本题考查了函数综合知识，函数综合题是初中数学中覆盖面最广、综合性最强的题型．近几年的中考压轴题多以函数综合题的形式出现．解决函数综合题的过程就是转化思想、数形结合思想、分类讨论思想、方程思想的应用过程．