题目内容
某中学为了了解本校初三学生体育成绩,从本校初三1200名学 生中随机抽取了部分学生进行测试,将测试成绩(满分100分,成绩均取整数)进行统计,绘制成如下图表(部分):
生中随机抽取了部分学生进行测试,将测试成绩(满分100分,成绩均取整数)进行统计,绘制成如下图表(部分):
| 组别 | 成绩 | 频数 | 频率 |
| 1 | 90.5~100.5 | 8 | 0.08 |
| 2 | 80.5~90.5 | m | 0.24 |
| 3 | 70.5~80.5 | 40 | n |
| 4 | 60.5~70.5 | 25 | 0.25 |
| 5 | 50.5~60.5 | 3 | 0.03 |
| 合计 |
(1)m=______,n=______;
(2)补全频数分布直方图;
(3)指出这组数据的“中位数”落在哪一组(不要求说明理由);
(4)若成绩80分以上的学生为优秀,请估计该校初三学生体育成绩优秀的人数.
解:(1)m=8÷0.08×0.24=24,
n=40÷(8÷0.08)=0.4;
故填24;0.4.
(2)如图所示;
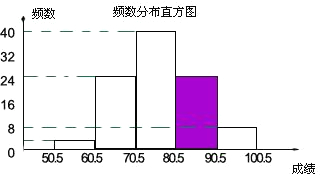
(3)∵抽取的部分学生的总人数为8÷0.08=100人,
∴依题意得这组数据的“中位数”落在第3组;
(4)估计该校初三学生体育成绩优秀的人数为
1200×(0.08+0.24)=384人.
分析:(1)首先用8÷0.08即可得到抽取的部分学生的总人数,然后用40除以总人数即可n,用总人数乘以0.24即可求出m;
(2)根据表格的信息就可以补全频数分布直方图;
(3)由于知道抽取的部分学生的总人数,根据中位数的定义和表格信息就可以得到这组数据的“中位数”落在哪一组;
(4)首先根据表格得到成绩80分以上的学生人数,然后除以总人数即得到抽取的部分学生的优秀率,再乘以1200即可求出该校初三学生体育成绩优秀的人数.
点评:本题主要考查读频数分布直方图的能力和利用统计图获取信息的能力.同时考查中位数的求法:给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.
n=40÷(8÷0.08)=0.4;
故填24;0.4.
(2)如图所示;

(3)∵抽取的部分学生的总人数为8÷0.08=100人,
∴依题意得这组数据的“中位数”落在第3组;
(4)估计该校初三学生体育成绩优秀的人数为
1200×(0.08+0.24)=384人.
分析:(1)首先用8÷0.08即可得到抽取的部分学生的总人数,然后用40除以总人数即可n,用总人数乘以0.24即可求出m;
(2)根据表格的信息就可以补全频数分布直方图;
(3)由于知道抽取的部分学生的总人数,根据中位数的定义和表格信息就可以得到这组数据的“中位数”落在哪一组;
(4)首先根据表格得到成绩80分以上的学生人数,然后除以总人数即得到抽取的部分学生的优秀率,再乘以1200即可求出该校初三学生体育成绩优秀的人数.
点评:本题主要考查读频数分布直方图的能力和利用统计图获取信息的能力.同时考查中位数的求法:给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.

练习册系列答案
相关题目
填写下列表格
| x | y | x2+2xy+y2 | (x+y)2 |
| 1 | 2 | ||
| +2 | -1 | ||
| 0 | 3 | ||
| … | … |
下列是甲乙两个水果店1---6月份的销售情况(单位:千克),为比较两个水果店销售的稳定性,应选择的统计图是
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | |
| 甲水果店 | 450 | 440 | 480 | 420 | 580 | 560 |
| 乙水果店 | 480 | 440 | 470 | 490 | 520 | 510 |
- A.条形图
- B.折线图
- C.扇形图
- D.以上都可以
一个多面体的面数(a)和这个多面体表面展开后得到的平面图形的顶点数(b),棱数(c)之间存在一定规律,如图1是正三棱柱的表面展开图,它原有5个面,展开后有10个顶点(重合的顶点只算一个),14条棱.

【探索发现】
(1)请在图2中用实线画出立方体的一种表面展开图;
(2)请根据图2你所画的图和图3的四棱锥表面展开图填写下表:
| 多面体 | 面数a | 展开图的顶点数b | 展开图的棱数c |
| 直三棱柱 | 5 | 10 | 14 |
| 四棱锥 | ______ | 8 | 12 |
| 立方体 | ______ | ______ | ______ |
【解决问题】
(4)已知一个多面体表面展开图有17条棱,且展开图的顶点数比原多面体的面数多2,则这个多面体的面数是多少?
 某种产品从生产流水线上下线后,需要包装人库,通常的办法是,流水线先工作一段时间,包装工人再开始工作.某次包装工人工作一段时间后,因临近下班,又抽调了一部分工人来帮忙,使包装人库的速度提高了一倍.如图是下线后待包装人库的产品数量y(件)与流水线开始工作时间t(h)的函数关系的图象.以下结论正确的有______.
某种产品从生产流水线上下线后,需要包装人库,通常的办法是,流水线先工作一段时间,包装工人再开始工作.某次包装工人工作一段时间后,因临近下班,又抽调了一部分工人来帮忙,使包装人库的速度提高了一倍.如图是下线后待包装人库的产品数量y(件)与流水线开始工作时间t(h)的函数关系的图象.以下结论正确的有______.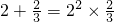 ,
,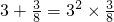 ,
,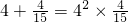 ,…,若
,…,若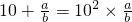 (a、b为正整数),计算a+b的值
(a、b为正整数),计算a+b的值 ,a2=
,a2= -
- ,a3=
,a3= ,a4=
,a4= ,….试猜想第n个等式(n为正整数):an=________.
,….试猜想第n个等式(n为正整数):an=________.