题目内容
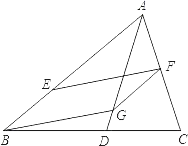
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是BC上任意一点,将线段AD绕点A逆时针方向旋转
,点D是BC上任意一点,将线段AD绕点A逆时针方向旋转![]() ,得到线段AE,连结EC.
,得到线段AE,连结EC.
![]() 依题意补全图形;
依题意补全图形;
![]() 求
求![]() 的度数;
的度数;
![]() 若
若![]() ,
,![]() ,将射线DA绕点D顺时针旋转
,将射线DA绕点D顺时针旋转![]() 交EC的延长线于点F,请写出求AF长的思路.
交EC的延长线于点F,请写出求AF长的思路.

【答案】(1)见解析;(2)90°;(3)解题思路见解析.
【解析】
(1)将线段AD绕点A逆时针方向旋转90°,得到线段AE,连结EC.
(2)先判定△ABD≌△ACE,即可得到![]() ,再根据
,再根据![]() ,即可得出
,即可得出![]() ;
;
(3)连接DE,由于△ADE为等腰直角三角形,所以可求![]() ;由
;由![]() ,
,![]() ,可求
,可求![]() 的度数和
的度数和![]() 的度数,从而可知DF的长;过点A作
的度数,从而可知DF的长;过点A作![]() 于点H,在Rt△ADH中,由
于点H,在Rt△ADH中,由![]() ,AD=1可求AH、DH的长;由DF、DH的长可求HF的长;在Rt△AHF中,由AH和HF,利用勾股定理可求AF的长.
,AD=1可求AH、DH的长;由DF、DH的长可求HF的长;在Rt△AHF中,由AH和HF,利用勾股定理可求AF的长.
解:![]() 如图,
如图,
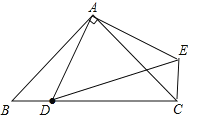
![]() 线段AD绕点A逆时针方向旋转
线段AD绕点A逆时针方向旋转![]() ,得到线段AE.
,得到线段AE.
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
在![]() 和
和![]() 中
中
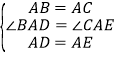 ,
,
![]() ≌
≌![]() .
.
![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
![]() ;
;
![]() Ⅰ
Ⅰ![]() 连接DE,由于
连接DE,由于![]() 为等腰直角三角形,所以可求
为等腰直角三角形,所以可求![]() ;
;
Ⅱ![]() 由
由![]() ,
,![]() ,可求
,可求![]() 的度数和
的度数和![]() 的度数,从而可知DF的长;
的度数,从而可知DF的长;
Ⅲ![]() 过点A作
过点A作![]() 于点H,在
于点H,在![]() 中,由
中,由![]() ,
,![]() 可求AH、DH的长;
可求AH、DH的长;
Ⅳ![]() 由DF、DH的长可求HF的长;
由DF、DH的长可求HF的长;
Ⅴ![]() 在
在![]() 中,由AH和HF,利用勾股定理可求AF的长.
中,由AH和HF,利用勾股定理可求AF的长.
故答案为:(1)见解析;(2)90°;(3)解题思路见解析.

【题目】某超市销售一种商品,每件的成本每千克18元,规定每千克售价不低于成本,且获利不得高于100%,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 39 | 38 | 37 |
销售量y(千克) | 20 | 22 | 24 | 26 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
(3)该超市若想每天销售利润不低于480元,请结合函数图象帮助超市确定产品的销售单价范围?