题目内容
已知:⊙O的直径为14cm,弦AB=10cm,点P为AB上一点,OP=5cm,则AP的长为分析:点P的位置有两种情况,根据垂径定理和勾股定理求解.
解答: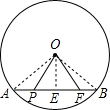 解:连接OA,OB,作OE⊥AB,垂足为E.点P的位置有两种情况:
解:连接OA,OB,作OE⊥AB,垂足为E.点P的位置有两种情况:
①当如图位置时,由垂径定理知,点E是AB的中点,AE=EB=
AB=5,OA=7,
由勾股定理得,OE=2
,PE=1,
∴AP=AE-PE=4cm;
②当点P在如图的点F位置时,可求得EF=1,所以AF=AE+EF=6cm.
故填4或6.
 解:连接OA,OB,作OE⊥AB,垂足为E.点P的位置有两种情况:
解:连接OA,OB,作OE⊥AB,垂足为E.点P的位置有两种情况:①当如图位置时,由垂径定理知,点E是AB的中点,AE=EB=
| 1 |
| 2 |
由勾股定理得,OE=2
| 6 |
∴AP=AE-PE=4cm;
②当点P在如图的点F位置时,可求得EF=1,所以AF=AE+EF=6cm.
故填4或6.
点评:本题利用了垂径定理和勾股定理求解,注意点P的位置有两种情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
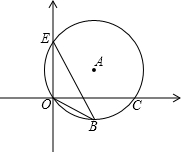 如图,点E、B、C在⊙A上,已知圆A的直径为1,BE是⊙A上的一条弦.则cos∠OBE=( )
如图,点E、B、C在⊙A上,已知圆A的直径为1,BE是⊙A上的一条弦.则cos∠OBE=( )| A、OB的长 | B、BE的长 | C、OE的长 | D、OC的长 |
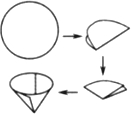 化学实验课上,小明用一张圆形滤纸做一个过滤器:先将圆形滤纸对折成半圆形,再对折成四分之一圆形,然后打开得到圆锥形过滤器.若已知圆形滤纸的直径为10cm,则滤纸重叠部分每层面积
化学实验课上,小明用一张圆形滤纸做一个过滤器:先将圆形滤纸对折成半圆形,再对折成四分之一圆形,然后打开得到圆锥形过滤器.若已知圆形滤纸的直径为10cm,则滤纸重叠部分每层面积