题目内容
如图1,以△ABC的边AB,AC为腰向外作等腰三角形ABE和ACD,且AB=AE,AC=AD,M为BC边的中点,MA的延长线交DE于N
(1)当∠BAC=∠BAE=∠CAD=90°时,线段AM线段DE的关系是
(2)如图2,当∠BAC≠90°时,探究线段AM与线段DE的关系.
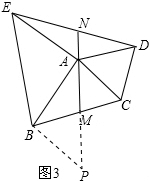
(3)如图3,当∠BAC≠90°时,∠BAE=α°,∠CAD=(180-α)°,则线段DE与AM的大小关系怎样?其夹角∠DNM是多少?请给出证明.

(1)当∠BAC=∠BAE=∠CAD=90°时,线段AM线段DE的关系是
DE=2AM且AM⊥DE
DE=2AM且AM⊥DE
.(2)如图2,当∠BAC≠90°时,探究线段AM与线段DE的关系.
(3)如图3,当∠BAC≠90°时,∠BAE=α°,∠CAD=(180-α)°,则线段DE与AM的大小关系怎样?其夹角∠DNM是多少?请给出证明.

分析:(1)先根据SAS证明△ABC≌△AED,得出BC=ED,∠ABM=∠AEN,再由直角三角形斜边上的中线等于斜边的一半得出BC=2AM,即DE=2AM;又由∠ABM=∠BAM,∠BAM+∠EAN=90°,得出∠AEN+∠EAN=90°,从而证明出AM⊥DE;
(2)延长AM到K,使MK=AM,连BK,根据SAS证明△ADE≌△BAK,得出DE=AK=2AM,∠BAK=∠AED,再证明∠AED+∠EAN=90°,从而有AM⊥DE;
(3)延长AM到P,使MP=MA,连接BP.根据SAS先证明△BMP≌△CMA,再证明△ABP≌△EAD,然后根据全等三角形的性质PA=DE=2AM,∠BPA=∠ADE=∠CAM,从而得出∠DNM=∠DAC=(180-α)°.
(2)延长AM到K,使MK=AM,连BK,根据SAS证明△ADE≌△BAK,得出DE=AK=2AM,∠BAK=∠AED,再证明∠AED+∠EAN=90°,从而有AM⊥DE;
(3)延长AM到P,使MP=MA,连接BP.根据SAS先证明△BMP≌△CMA,再证明△ABP≌△EAD,然后根据全等三角形的性质PA=DE=2AM,∠BPA=∠ADE=∠CAM,从而得出∠DNM=∠DAC=(180-α)°.
解答: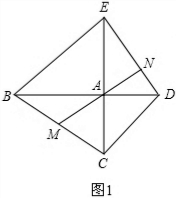 解:(1)DE=2AM且AM⊥DE.理由如下:
解:(1)DE=2AM且AM⊥DE.理由如下:
∵AB=AE,∠BAC=∠BAE=∠CAD=90°,AC=AD,
∴△ABC≌△AED(SAS),
∴BC=ED,∠ABM=∠AEN,
∵M为BC边的中点,
∴BC=2AM,
∴DE=2AM;
∴AM=BM=CM,
∴∠ABM=∠BAM,
∴∠BAM=∠AEN,
∵∠BAM+∠EAN=90°,
∴∠AEN+∠EAN=90°,
∴∠ANE=90°,
∴AM⊥DE;
即DE=2AM,AM⊥DE;
(2)DE=2AM且AM⊥ED.理由如下:
延长AM到K,使MK=AM,连BK,则ABKC是平行四边形,
∴AC=BK,∠ABK+∠BAC=180°,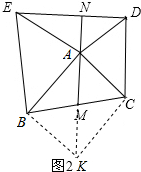
∵∠DAC=∠EAB=90°,
∴∠DAE+∠BAC=180°,
∴∠ABK=∠DAE,
又∵BK=AD,AB=AE,
∴△ABK≌△EAD(SAS),
∴AK=DE,∠BAK=∠AED.
∴DE=2AM,
∠AED+∠EAN=∠BAK+∠EAN=90°,
∴AM⊥DE,
即DE=2AM且AM⊥ED;
 (3)DE=2AM,∠DNM=(180-α)°.理由如下:
(3)DE=2AM,∠DNM=(180-α)°.理由如下:
延长AM到P,使MP=MA,连接BP.
又∵BM=CM,∠BMP=∠CMA,
∴△BMP≌△CMA(SAS),
∴BP=AC=AD;∠BPM=∠CAM;
且∠PBM=∠ACM,
∴BP∥AC,∠ABP+∠BAC=180°,
又∵∠BAE+∠CAD=α°+(180-α)°=180°,
∴∠DAE+∠BAC=180°,
∴∠ABP=∠DAE,
又∵BP=AD,AB=AE,
∴△ABP≌△EAD(SAS),
∴PA=DE,∠BPA=∠ADE=∠CAM,
∴DE=2AM,
∠DNM=180度-(∠ADE+∠DAN)=180度-(∠CAM+∠DAN)=∠DAC=(180-α)°.
即DE=2AM,∠DNM=(180-α)°.
故答案为:DE=2AM且AM⊥DE.
 解:(1)DE=2AM且AM⊥DE.理由如下:
解:(1)DE=2AM且AM⊥DE.理由如下:∵AB=AE,∠BAC=∠BAE=∠CAD=90°,AC=AD,
∴△ABC≌△AED(SAS),
∴BC=ED,∠ABM=∠AEN,
∵M为BC边的中点,
∴BC=2AM,
∴DE=2AM;
∴AM=BM=CM,
∴∠ABM=∠BAM,
∴∠BAM=∠AEN,
∵∠BAM+∠EAN=90°,
∴∠AEN+∠EAN=90°,
∴∠ANE=90°,
∴AM⊥DE;
即DE=2AM,AM⊥DE;
(2)DE=2AM且AM⊥ED.理由如下:
延长AM到K,使MK=AM,连BK,则ABKC是平行四边形,
∴AC=BK,∠ABK+∠BAC=180°,

∵∠DAC=∠EAB=90°,
∴∠DAE+∠BAC=180°,
∴∠ABK=∠DAE,
又∵BK=AD,AB=AE,
∴△ABK≌△EAD(SAS),
∴AK=DE,∠BAK=∠AED.
∴DE=2AM,
∠AED+∠EAN=∠BAK+∠EAN=90°,
∴AM⊥DE,
即DE=2AM且AM⊥ED;
 (3)DE=2AM,∠DNM=(180-α)°.理由如下:
(3)DE=2AM,∠DNM=(180-α)°.理由如下:延长AM到P,使MP=MA,连接BP.
又∵BM=CM,∠BMP=∠CMA,
∴△BMP≌△CMA(SAS),
∴BP=AC=AD;∠BPM=∠CAM;
且∠PBM=∠ACM,
∴BP∥AC,∠ABP+∠BAC=180°,
又∵∠BAE+∠CAD=α°+(180-α)°=180°,
∴∠DAE+∠BAC=180°,
∴∠ABP=∠DAE,
又∵BP=AD,AB=AE,
∴△ABP≌△EAD(SAS),
∴PA=DE,∠BPA=∠ADE=∠CAM,
∴DE=2AM,
∠DNM=180度-(∠ADE+∠DAN)=180度-(∠CAM+∠DAN)=∠DAC=(180-α)°.
即DE=2AM,∠DNM=(180-α)°.
故答案为:DE=2AM且AM⊥DE.
点评:本题主要考查了等腰三角形的性质,直角三角形斜边上中线的性质,全等三角形的判定与性质,综合性较强,从第一问到第三问,由特殊到一般,由浅入深,训练了学生思维,考查了学生分析问题、归纳问题、解决问题的能力.

练习册系列答案
相关题目



 16、如图,分别以△ABC的两条边为边作平行四边形,所做的平行四边形有
16、如图,分别以△ABC的两条边为边作平行四边形,所做的平行四边形有
 如图,分别以△ABC的边AB,AC向外作等边三角形ABD和等边三角形ACE,线段BE与CD相交于点O,连接OA.
如图,分别以△ABC的边AB,AC向外作等边三角形ABD和等边三角形ACE,线段BE与CD相交于点O,连接OA.