题目内容
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-4,0),B(2,0),与y轴交于点C(0,2).
(1)求抛物线对应的函数表达式;
(2)以AB为直径作⊙M,一直线经过点E(-1,-5),并且与⊙M相切,求该直线对应的函数表达式.

【答案】(1)y=-![]() x2-
x2-![]() x+2;(2)y=-
x+2;(2)y=-![]() x-
x-![]() 或y=
或y=![]() x-
x-![]() .
.
【解析】
(1)只需运用待定系数法就可解决问题;
(2)设过点E的直线与⊙M相切于点F,与x轴交于点N,连接MF,如图2,根据切线的性质可得MF⊥EN.易得M的坐标、ME、MF、EF的长,易证△MEF∽△NEM,根据相似三角形的性质可求出MN,从而得到点N的坐标,然后运用待定系数法就可解决问题.
(1)如图1,由题可得:
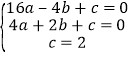 ,解得:
,解得: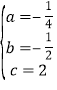 ,∴抛物线的解析式为y
,∴抛物线的解析式为y![]() x2
x2![]() x+2;
x+2;
(2)设过点E的直线与⊙M相切于点F,与x轴交于点N,连接MF,如图2,则有MF⊥EN.
∵A(﹣4,0),B(2,0),∴AB=6,MF=MB=MA=3,∴点M的坐标为(﹣4+3,0)即M(﹣1,0).
∵E(﹣1,﹣5),∴ME=5,∠EMN=90°.
在Rt△MFE中,EF![]() 4.
4.
∵∠MEF=∠NEM,∠MFE=∠EMN=90°,∴△MEF∽△NEM,∴![]() ,∴
,∴![]() ,∴NM
,∴NM![]() ,∴点N的坐标为(﹣1
,∴点N的坐标为(﹣1![]() ,0)或(﹣1
,0)或(﹣1![]() ,0),即(
,0),即(![]() ,0)或(
,0)或(![]() ,0).
,0).
设直线EN的解析式为y=px+q.
①当点N的坐标为(![]() ,0)时,
,0)时,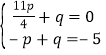 ,解得:
,解得: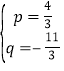 ,∴直线EN的解析式为y
,∴直线EN的解析式为y![]() .
.
②当点N的坐标为(![]() ,0)时,同理可得:直线EN的解析式为y
,0)时,同理可得:直线EN的解析式为y![]() .
.
综上所述:所求直线的解析式为y![]() 或y
或y![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目