题目内容
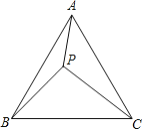
【题目】已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.
【答案】150°
【解析】
将△ABP旋转60°得到△BCQ,连接PQ,意证△BCQ≌△BAP,由于∠PBQ=60°,BP=BQ,易知△BPQ是等边三角形,从而有PQ=PB=4,而PC=5,CQ=3,由勾股定理逆定理可知△PQC是直角三角形,即∠PQC=90°,则可求出∠APB.
解:把△ABP绕点B顺时针旋转60°得到△BCQ,连接PQ.

由旋转可知,△BCQ≌△BAP
∴CQ=PA=3,∠BQC=∠APB
∵∠PBQ=60°,BP=BQ,
∴△BPQ是等边三角形,
∴PQ=PB=4,∠PQB=60°
∵PC=5
∴在△PQC中,,42+32=52
即PQ2+QC2=PC2,
∴△PQC是直角三角形
∴∠PQC=90°
∴∠BQC=∠PQB +∠PQC =60°+90°=150°,
∴∠APB=150°.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目