题目内容
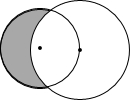 如图,一个半径为2
如图,一个半径为2| 2 |
8
8
.分析:连接AC,BC,DC,AB,求出AD和DC的平方和,求出AC的平方,根据勾股定理的逆定理得出∠ADC=90°,同理求出∠BDC=90°,推出A、D、B三点共线,即AB过D,根据AD=DC=BD求出∠ACB=90°,根据扇形ACB的面积和三角形ACB的面积求出弓形AmB的面积,求出半圆D的面积减去弓形AmB的面积即可得出答案.
解答:解: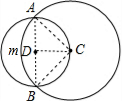
连接AC,BC,DC,AB,
∵⊙D过⊙C的圆心C,⊙D和⊙C交于A、B,
∴AD=BD=DC=2
,AC=4,
AD2+DC2=AC2=16,
∴∠ADC=90°,
同理∠BDC=90°,
∴A、D、B三点共线,
即D在两圆的公共弦AB上,
∵AD=CD=BD,
∴∠ACB=90°,
∴S弓形AmB=S扇形ACB-S△ACB=
-
×(2
+2
)×2
=4π-8,
∴阴影部分的面积是
×π×(2
)2-(4π-8)=8,
故答案为:8.

连接AC,BC,DC,AB,
∵⊙D过⊙C的圆心C,⊙D和⊙C交于A、B,
∴AD=BD=DC=2
| 2 |
AD2+DC2=AC2=16,
∴∠ADC=90°,
同理∠BDC=90°,
∴A、D、B三点共线,
即D在两圆的公共弦AB上,
∵AD=CD=BD,
∴∠ACB=90°,
∴S弓形AmB=S扇形ACB-S△ACB=
| 90π×42 |
| 360 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
∴阴影部分的面积是
| 1 |
| 2 |
| 2 |
故答案为:8.
点评:本题考查了勾股定理的逆定理、直角三角形的判定、扇形的面积、三角形的面积、平角的定义、相交两圆的性质等知识点,主要考查学生综合运用定理进行推理的能力,题目综合性比较强,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
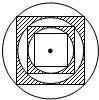 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
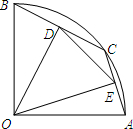 (2013•衡水模拟)如图,在半径为2的扇形AOB中,∠AOB=90°,点C是
(2013•衡水模拟)如图,在半径为2的扇形AOB中,∠AOB=90°,点C是
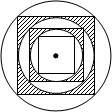 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是